sexta-feira, 12 de dezembro de 2008
quinta-feira, 4 de dezembro de 2008
Ainda os métodos de partilha no caso discreto


A tabela seguinte resume as características dos quatro métodos:
Hamilton / Jefferson / Adams / Webster
Viola regra da quota Não / Sim / Sim / Sim
Paradoxo Alabama Sim / Não / Não / Não
Paradoxo População Sim / Não / Não / Não
Paradoxo Novos-Estados Sim / Não / Não / Não
Favoritismo para Estados Grandes / Grandes / Pequenos / Pequenos
Note que cada um dos quatro métodos produz uma partilha diferente. Isto mostra claramente que os métodos são de facto todos diferentes. No entanto, é possível que dois métodos diferentes produzam partilhas idênticas.
Dos quatro métodos, o de Hamilton tem uma estreita ligação com as quotas standard (padrão), ao passo que os outros três (Jefferson, Adams, e Webster) estão baseados na filosofia que as quotas podem ser modificadas através da escolha apropriada do divisor. Apesar de alguns métodos serem claramente melhores que outros, nenhum deles é perfeito. Cada um deles viola a regra da quota ou então produz paradoxos.
sexta-feira, 21 de novembro de 2008
MÉTODOS DE PARTILHA NO CASO CONTÍNUO
- Método da divisão e escolha (usado na divisão em 2 partes)
- Método do divisor único (utilizado na divisão em 3 ou mais partes)
- Método do seleccionador único (usado na divisão em 3 ou mais partes)
- Método do último a diminuir
- Método livre de inveja
- Método da licitação secreta
- Método do divisor único (utilizado na divisão em 3 ou mais partes)
- Método do seleccionador único (usado na divisão em 3 ou mais partes)
- Método do último a diminuir
- Método livre de inveja
- Método da licitação secreta
quinta-feira, 20 de novembro de 2008
Método de Huntington - Hill
1º) Calcular o Divisor Padrão;
2º) Calcular a Quota Padrão de cada Estado;
3º) Aplica-se a Regra de Huntington-Hill:
I) Se a quota é um número inteiro, atribui-se ao interveniente essa quota.
II) Se a quota é um número não inteiro, calcula-se H = raíz quadrada de [L x(L+1)], sendo L o maior inteiro contido na quota, ou seja, a quota inferior;
III) Se H é menor que a quota, atribui-se a quota superior; se H é maior que a quota, atribui-se a quota inferior;
IV) Se o divisor padrão não permitir atribuir o número de mandatos previstos pelo processo, determina-se, por tentativa e erro, um divisor modificado até que seja possível atribuir o número exacto de mandatos.
2º) Calcular a Quota Padrão de cada Estado;
3º) Aplica-se a Regra de Huntington-Hill:
I) Se a quota é um número inteiro, atribui-se ao interveniente essa quota.
II) Se a quota é um número não inteiro, calcula-se H = raíz quadrada de [L x(L+1)], sendo L o maior inteiro contido na quota, ou seja, a quota inferior;
III) Se H é menor que a quota, atribui-se a quota superior; se H é maior que a quota, atribui-se a quota inferior;
IV) Se o divisor padrão não permitir atribuir o número de mandatos previstos pelo processo, determina-se, por tentativa e erro, um divisor modificado até que seja possível atribuir o número exacto de mandatos.
Método de Hamilton
1º) Calcular o Divisor Padrão;
2º) Calcular a Quota Padrão de cada Estado;
3º) Atribuir a cada Estado a sua Quota Inferior – número de lugares a que cada um tem direito;
4º) Se sobrarem lugares devem atribuir-se um a um, aos Estados por ordem decrescente da parte decimal da sua Quota Padrão.
2º) Calcular a Quota Padrão de cada Estado;
3º) Atribuir a cada Estado a sua Quota Inferior – número de lugares a que cada um tem direito;
4º) Se sobrarem lugares devem atribuir-se um a um, aos Estados por ordem decrescente da parte decimal da sua Quota Padrão.
Paradoxos
PARADOXO DE ALABAMA
Um aumento no número total de lugares a distribuir pode provocar uma perda de um lugar a um Estado.
PARADOXO DA POPULAÇÃO
O aumento da população de um Estado pode provocar a perda de um lugar a esse Estado.
PARADOXO DOS NOVOS ESTADOS
O número de lugares atribuídos aos Estados é afectado pela introdução de um novo Estado (assim como dos lugares que lhe pertencem)
Um aumento no número total de lugares a distribuir pode provocar uma perda de um lugar a um Estado.
PARADOXO DA POPULAÇÃO
O aumento da população de um Estado pode provocar a perda de um lugar a esse Estado.
PARADOXO DOS NOVOS ESTADOS
O número de lugares atribuídos aos Estados é afectado pela introdução de um novo Estado (assim como dos lugares que lhe pertencem)
MÉTODOS DE PARTILHA NO CASO DISCRETO
PROBLEMAS
1. Uma associação elege a cada dois anos, 10 representantes.Concorreram três listas, A,B e C que obtiveram 465, 265 e 279 votos respectivamente.
1.1. Qual é o número de mandatos atribuídos a cada lista utilizando o método de Hamilton?
1.2. Em seguida resolva o mesmo problema usando os métodos de :
1.2.1. Jefferson
1.2.2. Adams
1.1.3. Webster
1.2.4. Huntington-Hill
1. Uma associação elege a cada dois anos, 10 representantes.Concorreram três listas, A,B e C que obtiveram 465, 265 e 279 votos respectivamente.
1.1. Qual é o número de mandatos atribuídos a cada lista utilizando o método de Hamilton?
1.2. Em seguida resolva o mesmo problema usando os métodos de :
1.2.1. Jefferson
1.2.2. Adams
1.1.3. Webster
1.2.4. Huntington-Hill
Eleição do Presidente da República

O Presidente da República representa a República Portuguesa, garante a independência nacional, a unidade do Estado e o regular funcionamento das instituições democráticas e é, por inerência, Comandante Supremo das Forças Armadas.
Eleição
O Presidente da República é eleito por sufrágio universal, directo e secreto:
Dos cidadãos portugueses eleitores recenseados no território nacional;
Dos cidadãos portugueses residentes no estrangeiro, nas condições fixadas na Constituição e na lei.
Mandato
O mandato do Presidente da República é de cinco anos.
Elegibilidade e reelegibilidade
São elegíveis os cidadãos eleitores, portugueses de origem, maiores de 35 anos
Não é admitida a reeleição para um terceiro mandato consecutivo, nem durante o quinquénio imediatamente subsequente ao termo do segundo mandato consecutivo.
Se o Presidente da República renunciar ao cargo, não poderá candidatar-se nas eleições imediatas nem nas que se realizem no quinquénio imediatamente subsequente à renúncia.
Candidatura
As candidaturas para Presidente da República são propostas por um mínimo de 7 500 e um máximo de 15 000 cidadãos eleitores.
Sistema eleitoral
É eleito Presidente da República o candidato que obtiver mais de metade dos votos validamente expressos, não se considerando como tal os votos em branco.
Se nenhum dos candidatos obtiver esse número de votos, procede-se a um segundo sufrágio.
Ao segundo sufrágio concorrem apenas os dois candidatos mais votados que não tenham retirado a candidatura.
segunda-feira, 17 de novembro de 2008
Modelos populacionais - lista de exercícios
1.Admita que, ao longo dos séculos XIX e XX e dos primeiros anos do século XXI, a população de Portugal Continental, em milhões de habitantes, é dada,aproximadamente, por:
P(t) = 3,5 + 6,8 / (1 + 12,8 e^(- 0,036 t))
(Considere que t é medido em anos e que o instante t = 0 corresponde ao início do ano 1864).
a) De acordo com este modelo, qual será a população de Portugal Continental no final do ano de 2008?
(Apresente o resultado em milhões de habitantes, arredondado às décimas)
Nota: sempre que, nos cálculos intermédios,proceder a arredondamentos, conserve, no mínimo, 3 casas decimais.
b) Resolva o seguinte problema: de acordo com este modelo, em que ano a população de Portugal Continental foi de 3,7 milhões de habitantes?
Nota: sempre que, nos cálculos intermédios,arredondar valores conserve, no mínimo, 3 casas decimais.
2.O número de bactérias existentes numa determinada cultura é dado por:
N(t)= A×e^(kt)
em que t representa o número de horas decorridas após o momento inicial.
a) Sabendo que, inicialmente,havia 500 bactérias e que ao fim de 3 horas esse número duplicou,determine os valores de A e de k.
b) Para os valores obtidos na alínea anterior, determine um valor aproximado do número de bactérias ao fim de 5 horas.
P(t) = 3,5 + 6,8 / (1 + 12,8 e^(- 0,036 t))
(Considere que t é medido em anos e que o instante t = 0 corresponde ao início do ano 1864).
a) De acordo com este modelo, qual será a população de Portugal Continental no final do ano de 2008?
(Apresente o resultado em milhões de habitantes, arredondado às décimas)
Nota: sempre que, nos cálculos intermédios,proceder a arredondamentos, conserve, no mínimo, 3 casas decimais.
b) Resolva o seguinte problema: de acordo com este modelo, em que ano a população de Portugal Continental foi de 3,7 milhões de habitantes?
Nota: sempre que, nos cálculos intermédios,arredondar valores conserve, no mínimo, 3 casas decimais.
2.O número de bactérias existentes numa determinada cultura é dado por:
N(t)= A×e^(kt)
em que t representa o número de horas decorridas após o momento inicial.
a) Sabendo que, inicialmente,havia 500 bactérias e que ao fim de 3 horas esse número duplicou,determine os valores de A e de k.
b) Para os valores obtidos na alínea anterior, determine um valor aproximado do número de bactérias ao fim de 5 horas.
MODELOS POPULACIONAIS
domingo, 16 de novembro de 2008
Número cromático e coloração de um grafo
Número cromático de um grafo representa o menor número de cores necessárias para colorir os vértices de um grafo sem que vértices adjacentes tenham a mesma cor.
Consideremos os seguintes grafos:

Número de cores ( n ) = 2

Número de cores ( n ) = 4
Coloração em Grafo
Uma coloração de um grafo é uma atribuição de cores aos vértices, de modo que vértices adjacentes tenham cores distintas.
Um grafo G tem k-coloração se ele pode ser colorido com k cores.
• Um grafo G tem k-coloração significa que o grafo admite uma coloração mínima de k cores.Assim, definimos:
– O número cromático de G é k.
– G é k-cromático.
– c(G) = k .
Consideremos os seguintes grafos:

Número de cores ( n ) = 2

Número de cores ( n ) = 4
Coloração em Grafo
Uma coloração de um grafo é uma atribuição de cores aos vértices, de modo que vértices adjacentes tenham cores distintas.
Um grafo G tem k-coloração se ele pode ser colorido com k cores.
• Um grafo G tem k-coloração significa que o grafo admite uma coloração mínima de k cores.Assim, definimos:
– O número cromático de G é k.
– G é k-cromático.
– c(G) = k .
terça-feira, 4 de novembro de 2008
Os apertos de mão


No primeiro dia de aulas, o Afonso entrou no Bar da Escola e logo atrás
dele, sucessivamente, entraram mais seis colegas, todos seus amigos.
Cumprimentaram-se uns aos outros. O Afonso cumprimentou os seis amigos e todos se
cumprimentaram entre si.
Pensou o Afonso: “Quantos cumprimentos, ao todo, foram trocados entre os sete
colegas?”
E se ao grupo do Afonso se tivessem juntado os três colegas que faltaram, quantos cumprimentos, ao todo, teriam trocado entre si?
terça-feira, 28 de outubro de 2008
Teoria da Partilha Equilibrada
O Problema do Joalheiro
Malba Tahan, "O Homem que calculava" adaptado

Malba Tahan
Momentos depois chegávamos ao Mareco Dourado.
O dono da hospedaria chamava-se Salim e fora empregado do meu pai. Ao avistar-me gritou risonho:
-Alhah sobre ti, ( Deus te proteja) meu menino!Aguardo as tuas ordens agora e sempre!
Disse-lhe que precisava de um quarto para mim e para o meu amigo Beremiz Samir, o calculista, secretário do vizir Maluf.
- Esse homem é calculista?-indagou o velho Salim.-Chegou, então em momento oportuno para tirar-me de um embaraço. Acabo de ter uma séria divergência com um vendedor de jóias. Discutimos longo tempo e da nossa discussão resultou, afinal, um problema que não sabemos resolver.
Informadas de que um calculista havia chegado à hospedaria, várias pessoas aproximaram-se curiosas. O vendedor de jóais foi chamdo e declarou interessadíssimo na resolução do talconsoante a nossa combinação, pela hospedagem?
- Devo pagar apenas vinte e quatro dinares e meio!- replicou logo o mercador sírio.
Se para a venda de 200 eu pagaria 35, para a venda de 140 eu devo pagar 24 e meio!
-Está errado1-contrariou o velho Salim. - Pelas minhas contas são 28.
- Veja bem. Se para 100 eu deveria receber 20, para 140 devo receber 28. E vou provar
E o velho salim racicionou do seguinte modo:
- Se para 100 eu deveria receber 20, para 10 (que é a décima parte de 100) eu devria receber a décima parte de 20. problema.
- Qual é, afinal, a origem da dúvida?-perguntou Beremiz?
-Esse homem ( e a pontou o joalheiro) veio da Síria vender jóias em Bagdad; prometeu-me que pagaria, pela estadia, 20 dinares, se vendesse as jóais por 100 dinares, pagando 35 se as vendesse por 200.
Ao cabo de vários dias, tendo andado daqui para ali, acabou vendendo tudo por 140 dinares. Quanto deve pagar,
Qual é a décima parte de 20?
A décima parte de 20 é 2.
140 quantos 10 contém?
140 contém 14 vezes 10.
Logo, para 140, eu devo receber 14 vezes 2, que é igual a 28, como já disse.
E o velho Salim, depois de todos aqueles cálculos bradou enérgico:
-devo receber 28. É a conta certa.
-Calma meus amigos - interrompeu o calculista.- É preciso encarar as dúvidas com serenidade e mansidão. A precipitação conduz ao err e à discórdia. Os resultados que os senhores indicam estão errados, conforme vou provar.
E esclareceu o caso do seguinte modo:
- De acordo com a combinação feita, o sírio seria obrigado a pagar 20 dinares pela estadia, se vendesse as jóias por 100, e seria obrigado a pagar 35, se as vendesse por 200.
Temos assim:

Reparem que a diferença de 100, no preço de venda, corresponde a uma diferença de 15 no preço total da estadia, certo?
- Claro como leite de camela!- assentiram os dois.
- Ora - prosseguiu o calculista - se o acréscimo de 100 na venda traria um aumento de 15 na estadia, eu pergunto:- Qual será o aumento da estadia para o acréscimo de 40 na venda?
Se a diferença fosse 20 (que é um quinto de 100) , o aumento da estadia seria de 3 ( pois 3 é um quinto de 15).
Para a diferença de 40 ( que é o dobro de 20), o acréscimo da estadia deverá ser de 6.
O pagamento correspondente a 140 é, portanto, de 26.
- Meu amigo! os números na simplicidade como se apresentam, iludem, não raro , os mais avisados.
As proporções que nos parecem perfeitas, estão por vezes, falseadas pelo erro.
Da incerteza dos cálculos é que resulta o indiscutível prestigío da Matemática.
... O sírio pagou 26 dinares e não 24 e meio e ofereceu ao talentoso Beremiz, um anel de ouro...
problema retirado do blog Matemática na Cidadela
Malba Tahan, "O Homem que calculava" adaptado

Malba Tahan
Momentos depois chegávamos ao Mareco Dourado.
O dono da hospedaria chamava-se Salim e fora empregado do meu pai. Ao avistar-me gritou risonho:
-Alhah sobre ti, ( Deus te proteja) meu menino!Aguardo as tuas ordens agora e sempre!
Disse-lhe que precisava de um quarto para mim e para o meu amigo Beremiz Samir, o calculista, secretário do vizir Maluf.
- Esse homem é calculista?-indagou o velho Salim.-Chegou, então em momento oportuno para tirar-me de um embaraço. Acabo de ter uma séria divergência com um vendedor de jóias. Discutimos longo tempo e da nossa discussão resultou, afinal, um problema que não sabemos resolver.
Informadas de que um calculista havia chegado à hospedaria, várias pessoas aproximaram-se curiosas. O vendedor de jóais foi chamdo e declarou interessadíssimo na resolução do talconsoante a nossa combinação, pela hospedagem?
- Devo pagar apenas vinte e quatro dinares e meio!- replicou logo o mercador sírio.
Se para a venda de 200 eu pagaria 35, para a venda de 140 eu devo pagar 24 e meio!
-Está errado1-contrariou o velho Salim. - Pelas minhas contas são 28.
- Veja bem. Se para 100 eu deveria receber 20, para 140 devo receber 28. E vou provar
E o velho salim racicionou do seguinte modo:
- Se para 100 eu deveria receber 20, para 10 (que é a décima parte de 100) eu devria receber a décima parte de 20. problema.
- Qual é, afinal, a origem da dúvida?-perguntou Beremiz?
-Esse homem ( e a pontou o joalheiro) veio da Síria vender jóias em Bagdad; prometeu-me que pagaria, pela estadia, 20 dinares, se vendesse as jóais por 100 dinares, pagando 35 se as vendesse por 200.
Ao cabo de vários dias, tendo andado daqui para ali, acabou vendendo tudo por 140 dinares. Quanto deve pagar,
Qual é a décima parte de 20?
A décima parte de 20 é 2.
140 quantos 10 contém?
140 contém 14 vezes 10.
Logo, para 140, eu devo receber 14 vezes 2, que é igual a 28, como já disse.
E o velho Salim, depois de todos aqueles cálculos bradou enérgico:
-devo receber 28. É a conta certa.
-Calma meus amigos - interrompeu o calculista.- É preciso encarar as dúvidas com serenidade e mansidão. A precipitação conduz ao err e à discórdia. Os resultados que os senhores indicam estão errados, conforme vou provar.
E esclareceu o caso do seguinte modo:
- De acordo com a combinação feita, o sírio seria obrigado a pagar 20 dinares pela estadia, se vendesse as jóias por 100, e seria obrigado a pagar 35, se as vendesse por 200.
Temos assim:
Reparem que a diferença de 100, no preço de venda, corresponde a uma diferença de 15 no preço total da estadia, certo?
- Claro como leite de camela!- assentiram os dois.
- Ora - prosseguiu o calculista - se o acréscimo de 100 na venda traria um aumento de 15 na estadia, eu pergunto:- Qual será o aumento da estadia para o acréscimo de 40 na venda?
Se a diferença fosse 20 (que é um quinto de 100) , o aumento da estadia seria de 3 ( pois 3 é um quinto de 15).
Para a diferença de 40 ( que é o dobro de 20), o acréscimo da estadia deverá ser de 6.
O pagamento correspondente a 140 é, portanto, de 26.
- Meu amigo! os números na simplicidade como se apresentam, iludem, não raro , os mais avisados.
As proporções que nos parecem perfeitas, estão por vezes, falseadas pelo erro.
Da incerteza dos cálculos é que resulta o indiscutível prestigío da Matemática.
... O sírio pagou 26 dinares e não 24 e meio e ofereceu ao talentoso Beremiz, um anel de ouro...
problema retirado do blog Matemática na Cidadela
domingo, 28 de setembro de 2008
quinta-feira, 18 de setembro de 2008
O Dilema do Prisioneiro

imagem retirada de psicoevolucionistaclinica.blogspot.com
Dois criminosos, A e B são presos. Não havendo provas suficientes para os condenar, a polícia separa-os em celas sem comunicação e propõe aos dois o seguinte:
- Se um deles denunciar o outro e este permanecer calado, o denunciante sai livre e o outro, denunciado, apanha uma pena de 10 anos.
- Se ambos os prisioneiros denunciarem o parceiro, apanham uma pena de 5 anos.
- Se ambos permanecerem calados, apanham 6 meses de cadeia.
Quem tem vantagem A ou B?
Terão vantagem se ambos forem denunciantes? Como pensarão para denunciarem? O para não o fazerem?
Qual será então a melhor estratégia, a 1ª, a 2ª ou a 3ª ?
.
Pensa neste dilema e na frase
" Nem sempre a decisão mais racional é a mais vantajosa"
- do matemático Ian Stewart
Problema retirado do blogue Matemática na Cidadela e colocado por Margarida Pinto Teixeira
sábado, 13 de setembro de 2008
segunda-feira, 1 de setembro de 2008
Método de Hondt - breve história
MÉTODO DE HONDT
Em Portugal, as leis eleitorais da Assembleia da República, Assembleias Legislativas Regionais, Autarquias Locais e Parlamento Europeu seguem o sistema de representação proporcional e utilizam o método de Hondt.
Hondt
Victor D'Hondt ( Gand, 1841-1901 ), jurista belga e professor de direito civil na Universidade de Gand ( Ghent ), adepto da representação proporcional [ consiste na repartição dos mandatos pelos partidos, proporcionalmente à importância da respectiva votação ], concebeu o método que leva o seu nome. O procedimento de atribuição pela 'média mais alta', produz resultados idênticos aos do método de Hondt. As suas obras mais importantes são:
-"La représentation proportionnelle des partis par un électeur", Gand,1878.
"Système pratique et raisonné de représentation proportionelle", Bruxelles, Muquardt, 1882.
-"Exposé du système pratique de représentation proportionnelle", Gand, Imprimerie Eug. Vanderhaeghen, 1885.
-"Tables de division des nombres 1 à 400 par 1 à 31 et 401 à 1000 par 1 à 13 pour la répartition proportionnelle des sièges en matière électorale avec exposé de la méthode", Gand, A Siffer, 1900.
Na Bélgica este sistema foi aplicado pela primeira vez nas eleições parlamentares de 1900.
Em Portugal, em 1909/1910, através de proposta de reforma eleitoral e em artigos na imprensa [ Leão Azedo, "A representação proporcional", Alma Nacional, nº 21, 30-Jun-1910 ], o Partido Republicano (PR) advogava a utilização da representação proporcional. Seria contemplada na Lei Eleitoral de 14-Março-1910 para os círculos de Lisboa e Porto. Face à disparidade dos resultados eleitorais, o PR obteve nas duas cidades mais de 93 % dos votos, o método de Hondt acabou por não ter aplicação prática. A legislação posterior, Lei nº 3, de 3-Julho-1913, terminaria com a inovação, regressando ao sistema de lista incompleta da anterior legislação monárquica e que se manteria até 1925.
Entre as características do método de Hondt importa assinalar o encorajamento à formação de coligações, uma vez que o agrupamento de partidos leva a conseguir maior número de mandatos do que se concorressem isoladamente. Favorece no entanto os grandes partidos, não satisfazendo o critério da quota. A análise dos resultados eleitorais em Portugal, após 1975 mostra isso mesmo.
A comissão de redacção da primeira lei eleitoral após a revolução de 25 de Abril de 1974 ( Decreto-Lei nº 621-C/74, de 15-Nov ) , " ... optou - por unanimidade - pelo método de Hondt por ser aquele que melhor poderá traduzir a vontade do corpo eleitoral, ... " ( Relatório da Eleição para a Assembleia Constituinte 1975, volume I - Projecto de Lei Eleitoral, Ministério da Administração Interna, Secretariado Técnico dos Assuntos Políticos ).
O nº 1 do artigo 155º [ actual 149º, com nova redacção ] da Constituição da República (1976) estabelece que « Os Deputados são eleitos segundo o sistema de representação proporcional e o método da média mais alta de Hondt » foi aprovado com 31 abstenções ( PCP, MDP, UDP e oito Deputados ex-PPD ) - in "Constituição da República Portuguesa 1976 (anotada), Victor Silva Lopes, [Lisboa], Editus, 1976.
Em Portugal, as leis eleitorais da Assembleia da República, Assembleias Legislativas Regionais, Autarquias Locais e Parlamento Europeu seguem o sistema de representação proporcional e utilizam o método de Hondt.
Hondt
Victor D'Hondt ( Gand, 1841-1901 ), jurista belga e professor de direito civil na Universidade de Gand ( Ghent ), adepto da representação proporcional [ consiste na repartição dos mandatos pelos partidos, proporcionalmente à importância da respectiva votação ], concebeu o método que leva o seu nome. O procedimento de atribuição pela 'média mais alta', produz resultados idênticos aos do método de Hondt. As suas obras mais importantes são:
-"La représentation proportionnelle des partis par un électeur", Gand,1878.
"Système pratique et raisonné de représentation proportionelle", Bruxelles, Muquardt, 1882.
-"Exposé du système pratique de représentation proportionnelle", Gand, Imprimerie Eug. Vanderhaeghen, 1885.
-"Tables de division des nombres 1 à 400 par 1 à 31 et 401 à 1000 par 1 à 13 pour la répartition proportionnelle des sièges en matière électorale avec exposé de la méthode", Gand, A Siffer, 1900.
Na Bélgica este sistema foi aplicado pela primeira vez nas eleições parlamentares de 1900.
Em Portugal, em 1909/1910, através de proposta de reforma eleitoral e em artigos na imprensa [ Leão Azedo, "A representação proporcional", Alma Nacional, nº 21, 30-Jun-1910 ], o Partido Republicano (PR) advogava a utilização da representação proporcional. Seria contemplada na Lei Eleitoral de 14-Março-1910 para os círculos de Lisboa e Porto. Face à disparidade dos resultados eleitorais, o PR obteve nas duas cidades mais de 93 % dos votos, o método de Hondt acabou por não ter aplicação prática. A legislação posterior, Lei nº 3, de 3-Julho-1913, terminaria com a inovação, regressando ao sistema de lista incompleta da anterior legislação monárquica e que se manteria até 1925.
Entre as características do método de Hondt importa assinalar o encorajamento à formação de coligações, uma vez que o agrupamento de partidos leva a conseguir maior número de mandatos do que se concorressem isoladamente. Favorece no entanto os grandes partidos, não satisfazendo o critério da quota. A análise dos resultados eleitorais em Portugal, após 1975 mostra isso mesmo.
A comissão de redacção da primeira lei eleitoral após a revolução de 25 de Abril de 1974 ( Decreto-Lei nº 621-C/74, de 15-Nov ) , " ... optou - por unanimidade - pelo método de Hondt por ser aquele que melhor poderá traduzir a vontade do corpo eleitoral, ... " ( Relatório da Eleição para a Assembleia Constituinte 1975, volume I - Projecto de Lei Eleitoral, Ministério da Administração Interna, Secretariado Técnico dos Assuntos Políticos ).
O nº 1 do artigo 155º [ actual 149º, com nova redacção ] da Constituição da República (1976) estabelece que « Os Deputados são eleitos segundo o sistema de representação proporcional e o método da média mais alta de Hondt » foi aprovado com 31 abstenções ( PCP, MDP, UDP e oito Deputados ex-PPD ) - in "Constituição da República Portuguesa 1976 (anotada), Victor Silva Lopes, [Lisboa], Editus, 1976.
A Página da Educação- Artigo
A Página da Educação Arquivo - Artigo
Matemática Aplicada às Ciências Sociais
Deveriam ser estudados em detalhe quais os conhecimentos e capacidades importantes para a vida de um cidadão do século XXI [esse exercício seria certamente útil a outros níveis como a educação de adultos] e esse estudo deveria ter consequências directas na elaboração do plano de estudos e na definição dos conteúdos de cada disciplina.
Valerá mesmo a pena ensinar Matemática a todos os jovens se o insucesso é tão alto? Não será preferível, pelo menos para alguns alunos do Ensino Secundário, substituir essa disciplina por outra mais adequada aos “interesses” destes alunos?
As finalidades, os conteúdos e as metodologias de trabalho propostas nos programas oficiais de cada disciplina ficam normalmente num segundo plano quando se discutem os objectivos de cada ciclo de estudos. Muitas intenções piedosas são escritas sobre o interesse e importância de cada disciplina para o futuro dos alunos: “é muito importante os alunos saberem X”, “é fundamental que os alunos entendam Y”, etc., etc.. Será mesmo importante?
Quando se afirma que uma determinada disciplina é “fundamental”, a argumentação fica-se muito por generalidades do tipo “importante para formar o raciocínio” como se várias disciplinas não desempenhassem esse mesmo papel. E as consequências são as visíveis: na realidade não há investimento nessas disciplinas apelidadas de “fundamentais” e, por exemplo, no ano lectivo 2004-2005, a disciplina de Matemática sofreu mesmo uma séria “machadada” com a eliminação do desdobramento de um tempo lectivo, inviabilizando um trabalho de índole mais prática e impedindo os professores de acompanhar melhor os alunos nas suas muitas dificuldades.
Entendo que é preciso definir critérios claros para incluir uma disciplina ou um conteúdo de uma disciplina num determinado plano de estudos. E, no caso do Ensino Secundário, um dos critérios deve ser o da preparação do jovem para uma participação activa, consciente e autónoma no mundo actual. Deveriam ser estudados em detalhe quais os conhecimentos e capacidades importantes para a vida de um cidadão do século XXI (esse exercício seria certamente útil a outros níveis como a educação de adultos); e esse estudo deveria ter consequências directas na elaboração do plano de estudos e na definição dos conteúdos de cada disciplina. Um trabalho como “Educação para a Cidadania - Cursos gerais e Tecnológicos” elaborado por uma equipa coordenada por José Manuel Pureza e editado em 2001 pelo Departamento do Ensino Secundário do Ministério da Educação parece ter passado totalmente despercebido (e, claro, não teve consequências).
Por exemplo, os alunos dos Cursos de Ciências Sociais e Humanas e de Línguas e Literaturas do actual Ensino Secundário precisam de estudar Matemática (isto é, de mais Matemática, para além daquela que estudaram no Ensino Básico)?
Entendo que sim, embora precisem de Matemática diferente da de outros alunos; esses alunos, na sua vida adulta, tanto profissional como de cidadãos eleitores e elegíveis, vão ser confrontados com inúmeras questões que envolvem aspectos matemáticos: eleições, partilhas, correlações, evolução segundo determinadas leis (exponencial,...), grafos, probabilidades, inferências e previsões, etc. Parece-me por isso fundamental que estes alunos possam ser capazes de fazer uma abordagem matemática (do concreto para o abstracto e, inversamente aplicar o abstracto ao concreto) de situações que identifiquem como interessantes e significativas, que desenvolvam a sua capacidade de formular e resolver matematicamente problemas e que desenvolvam a tão importante capacidade de comunicação de ideias matemáticas. Mais do que querer que os estudantes dominem questões técnicas e de pormenor, é bom que os estudantes tenham experiências matemáticas significativas que lhes permitam saber apreciar devidamente a importância das abordagens matemáticas nas suas futuras actividades.
É por isso lamentável que uma disciplina como “Matemática Aplicada às Ciências Sociais”, que pretende responder às preocupações enunciadas, seja opcional no Curso de Ciências Sociais (e por isso nem sequer existe em muitas Escolas Secundárias) e nem sequer seja opção no Curso de Línguas e Literaturas. Estes alunos não irão ser cidadãos completos num século XXI cada vez mais exigente em termos científicos e tecnológicos.
Matemática Aplicada às Ciências Sociais
Deveriam ser estudados em detalhe quais os conhecimentos e capacidades importantes para a vida de um cidadão do século XXI [esse exercício seria certamente útil a outros níveis como a educação de adultos] e esse estudo deveria ter consequências directas na elaboração do plano de estudos e na definição dos conteúdos de cada disciplina.
Valerá mesmo a pena ensinar Matemática a todos os jovens se o insucesso é tão alto? Não será preferível, pelo menos para alguns alunos do Ensino Secundário, substituir essa disciplina por outra mais adequada aos “interesses” destes alunos?
As finalidades, os conteúdos e as metodologias de trabalho propostas nos programas oficiais de cada disciplina ficam normalmente num segundo plano quando se discutem os objectivos de cada ciclo de estudos. Muitas intenções piedosas são escritas sobre o interesse e importância de cada disciplina para o futuro dos alunos: “é muito importante os alunos saberem X”, “é fundamental que os alunos entendam Y”, etc., etc.. Será mesmo importante?
Quando se afirma que uma determinada disciplina é “fundamental”, a argumentação fica-se muito por generalidades do tipo “importante para formar o raciocínio” como se várias disciplinas não desempenhassem esse mesmo papel. E as consequências são as visíveis: na realidade não há investimento nessas disciplinas apelidadas de “fundamentais” e, por exemplo, no ano lectivo 2004-2005, a disciplina de Matemática sofreu mesmo uma séria “machadada” com a eliminação do desdobramento de um tempo lectivo, inviabilizando um trabalho de índole mais prática e impedindo os professores de acompanhar melhor os alunos nas suas muitas dificuldades.
Entendo que é preciso definir critérios claros para incluir uma disciplina ou um conteúdo de uma disciplina num determinado plano de estudos. E, no caso do Ensino Secundário, um dos critérios deve ser o da preparação do jovem para uma participação activa, consciente e autónoma no mundo actual. Deveriam ser estudados em detalhe quais os conhecimentos e capacidades importantes para a vida de um cidadão do século XXI (esse exercício seria certamente útil a outros níveis como a educação de adultos); e esse estudo deveria ter consequências directas na elaboração do plano de estudos e na definição dos conteúdos de cada disciplina. Um trabalho como “Educação para a Cidadania - Cursos gerais e Tecnológicos” elaborado por uma equipa coordenada por José Manuel Pureza e editado em 2001 pelo Departamento do Ensino Secundário do Ministério da Educação parece ter passado totalmente despercebido (e, claro, não teve consequências).
Por exemplo, os alunos dos Cursos de Ciências Sociais e Humanas e de Línguas e Literaturas do actual Ensino Secundário precisam de estudar Matemática (isto é, de mais Matemática, para além daquela que estudaram no Ensino Básico)?
Entendo que sim, embora precisem de Matemática diferente da de outros alunos; esses alunos, na sua vida adulta, tanto profissional como de cidadãos eleitores e elegíveis, vão ser confrontados com inúmeras questões que envolvem aspectos matemáticos: eleições, partilhas, correlações, evolução segundo determinadas leis (exponencial,...), grafos, probabilidades, inferências e previsões, etc. Parece-me por isso fundamental que estes alunos possam ser capazes de fazer uma abordagem matemática (do concreto para o abstracto e, inversamente aplicar o abstracto ao concreto) de situações que identifiquem como interessantes e significativas, que desenvolvam a sua capacidade de formular e resolver matematicamente problemas e que desenvolvam a tão importante capacidade de comunicação de ideias matemáticas. Mais do que querer que os estudantes dominem questões técnicas e de pormenor, é bom que os estudantes tenham experiências matemáticas significativas que lhes permitam saber apreciar devidamente a importância das abordagens matemáticas nas suas futuras actividades.
É por isso lamentável que uma disciplina como “Matemática Aplicada às Ciências Sociais”, que pretende responder às preocupações enunciadas, seja opcional no Curso de Ciências Sociais (e por isso nem sequer existe em muitas Escolas Secundárias) e nem sequer seja opção no Curso de Línguas e Literaturas. Estes alunos não irão ser cidadãos completos num século XXI cada vez mais exigente em termos científicos e tecnológicos.
quarta-feira, 4 de junho de 2008
Tabelas do IMT - 2008
Tabela para cálculo do IMT em 2008, aplicável no Continente
É calculado multiplicando a "Taxa Marginal" pelo valor de transacção do imóvel constante do CPCV e da Escritura (ou sobre o valor patrimonial tributário constante da matriz predial, se for maior) e deduzindo depois o "Valor a Abater
Continente
Tabela prática para cálculo do IMT para 2008 – (Habitação Própria e Permanente)
Valor para cálculo do Imposto s/ Transmissões (IMT)/Taxa marginal/Parcela a abater
até 87.500 euros 0% 0 euros
de 87.500,01 até 119.700 euros 2% 1.750,00 euros
de 119.700,01 até 163.200 euros 5% 5.341,00 euros
de 163.200,01 até 272.000 euros 7% 8.605,00 euros
de 272.001 até 521.700 euros 8% 11.325,00 euros
superior a 521.700,01 euros 6% 0 euros
Tabela prática para cálculo do IMT para 2008 – (Habitação Secundária e Habitação para Arrendamento)
Valor para cálculo do Imposto s/ Transmissões (IMT)/Taxa marginal/Parcela a abater
até 87.500 euros 0% 0 euros
de 87.500,01 até 119.700 euros 2% 875,00 euros
de 119.700,01 até 163.200 euros 5% 4.466,00 euros
de 163.200,01 até 272.000 euros 7% 7.730,00 euros
de 272.001 até 543.900 euros 8% 10.450,00 euros
superior a 543.900,01 euros 6% 0 euros
Tabela para cálculo do IMT em 2008, aplicável no Regiões Autónomas
É calculado multiplicando a "Taxa Marginal" pelo valor de transacção do imóvel constante do CPCV e da Escritura (ou sobre o valor patrimonial tributário constante da matriz predial, se for maior) e deduzindo depois o "Valor a Abater".
Tabela prática para cálculo do IMT para 2008 – (Habitação Própria e Permanente)
Valor para cálculo do Imposto s/ Transmissões (IMT)/Taxa marginal/Parcela a abater
até 109.375 euros 0% 0 euros
de 109.375,01 até 149.625 euros 2% 2.187,50 euros
de 149.625,01 até 204.000 euros 5% 6.676,25 euros
de 204.000,01 até 340.000 euros 7% 10.756,25 euros
de 340.001 até 679.875 euros 8% 14.156,25 euros
superior a 679.875,01 euros 6% 0 euros
Tabela prática para cálculo do IMT para 2008 – (Habitação Secundária e Habitação para Arrendamento)
Valor para cálculo do Imposto s/ Transmissões (IMT)/ Taxa marginal/ Parcela a abater
até 109.375 euros 0% 0 euros
de 109.375,01 até 149.625 euros 2% 1.093,75 euros
de 149.625,01 até 204.000 euros 5% 5.582,50 euros
de 204.000,01 até 340.000 euros 7% 9.662,50 euros
de 340.001 até 652.125 euros 8% 13.062,50 euros
superior a 652.125,01 euros 6% 0 euros
É calculado multiplicando a "Taxa Marginal" pelo valor de transacção do imóvel constante do CPCV e da Escritura (ou sobre o valor patrimonial tributário constante da matriz predial, se for maior) e deduzindo depois o "Valor a Abater
Continente
Tabela prática para cálculo do IMT para 2008 – (Habitação Própria e Permanente)
Valor para cálculo do Imposto s/ Transmissões (IMT)/Taxa marginal/Parcela a abater
até 87.500 euros 0% 0 euros
de 87.500,01 até 119.700 euros 2% 1.750,00 euros
de 119.700,01 até 163.200 euros 5% 5.341,00 euros
de 163.200,01 até 272.000 euros 7% 8.605,00 euros
de 272.001 até 521.700 euros 8% 11.325,00 euros
superior a 521.700,01 euros 6% 0 euros
Tabela prática para cálculo do IMT para 2008 – (Habitação Secundária e Habitação para Arrendamento)
Valor para cálculo do Imposto s/ Transmissões (IMT)/Taxa marginal/Parcela a abater
até 87.500 euros 0% 0 euros
de 87.500,01 até 119.700 euros 2% 875,00 euros
de 119.700,01 até 163.200 euros 5% 4.466,00 euros
de 163.200,01 até 272.000 euros 7% 7.730,00 euros
de 272.001 até 543.900 euros 8% 10.450,00 euros
superior a 543.900,01 euros 6% 0 euros
Tabela para cálculo do IMT em 2008, aplicável no Regiões Autónomas
É calculado multiplicando a "Taxa Marginal" pelo valor de transacção do imóvel constante do CPCV e da Escritura (ou sobre o valor patrimonial tributário constante da matriz predial, se for maior) e deduzindo depois o "Valor a Abater".
Tabela prática para cálculo do IMT para 2008 – (Habitação Própria e Permanente)
Valor para cálculo do Imposto s/ Transmissões (IMT)/Taxa marginal/Parcela a abater
até 109.375 euros 0% 0 euros
de 109.375,01 até 149.625 euros 2% 2.187,50 euros
de 149.625,01 até 204.000 euros 5% 6.676,25 euros
de 204.000,01 até 340.000 euros 7% 10.756,25 euros
de 340.001 até 679.875 euros 8% 14.156,25 euros
superior a 679.875,01 euros 6% 0 euros
Tabela prática para cálculo do IMT para 2008 – (Habitação Secundária e Habitação para Arrendamento)
Valor para cálculo do Imposto s/ Transmissões (IMT)/ Taxa marginal/ Parcela a abater
até 109.375 euros 0% 0 euros
de 109.375,01 até 149.625 euros 2% 1.093,75 euros
de 149.625,01 até 204.000 euros 5% 5.582,50 euros
de 204.000,01 até 340.000 euros 7% 9.662,50 euros
de 340.001 até 652.125 euros 8% 13.062,50 euros
superior a 652.125,01 euros 6% 0 euros
quarta-feira, 28 de maio de 2008
Cansado de Pagar Juros? Entenda os Cálculos de Juros

Juro é um valor acrescido de uma aplicação financeira, ou seja, uma quantia em dinheiro que deve ser paga por um devedor (o que pede emprestado), pela utilização de dinheiro de um credor (aquele que empresta).
Existem dois tipos de juros:
Juros Simples - São acréscimos que são somados ao capital inicial no final da aplicação.
Juros Compostos - São acréscimos somados ao capital, ao fim de cada período de aplicação, formando com esta soma um novo capital.
A grande diferença dos juros é que no final da aplicação quem financia através de juros simples obtem um montante (valor total a pagar) inferior ao que financia por juros compostos.
A fórmula do Juro Simples é: j = C. i. n onde:
j = juros, C = capital, i = taxa de juro, n = período de tempo.
Exemplo:
Uma pessoa empresta a outra a quantia de € 2.000,00, a juros simples, pelo prazo de 3 meses, à taxa de 3% ao mês. Quanto deverá ser pago de juros?
Antes de iniciarmos a resolução deste problema, devemos descobrir, o que é o quê, ou seja, quais dados do problema.
Capital aplicado (C) : € 2.000,00
Tempo de aplicação (n) : 3 meses
Taxa de juro (i): 3% ou 0,03 ao mês (a.m.)
Fazendo o cálculo, teremos:
J = c . i. n → J = 2.000 x 3 x 0,03 → € 180,00
Ao final do empréstimo, essa pessoa pagará € 180,00 de juros.
Observe-se , que se fizermos o cálculo mês a mês, o valor dos juros será de € 60,00 por mês e esse valor será somado mês a mês pois nunca mudará.
A fórmula dos Juros Compostos é: M = C. (1 + i)^n
onde:
M = capital acumulado, C = Capital investido, i = taxa de juro, n = período de tempo.
Considerando o mesmo problema anterior
Fazendo os cálculos, teremos:
M = 2.000 . ( 1 + 0,03)³ → M = 2.000 . (1,03)³ → M = € 2.185,45
segunda-feira, 12 de maio de 2008
sábado, 10 de maio de 2008
sexta-feira, 9 de maio de 2008
Exercícios sobre os modelos de probabilidade

Problema 1
Acredita-se que 28% dos moradores de um bairro das proximidades de uma grande indústria siderúrgica tem alergia aos poluentes lançados ao ar. Admitindo que este percentual de alérgicos é real, calcule a probabilidade de que pelo menos 4 moradores tenham alergia entre 15 seleccionados ao acaso. E qual a probabilidade de serem 6 os afectados pelo surto alérgico? De entre os 400 moradores do bairro, qual o número esperado de moradores afectados com alergia?
Problema 2
O quociente de inteligência (QI) dos alunos admitidos em certa faculdade de medicina tem distribuição normal com média de 114 e desvio padrão de 10. Encontre:
a) O número de indivíduos com QI maior que 124;
b) A probabilidade de um indivíduo tomado ao acaso tenha QI entre 104 e 114;
c) P(94 < X < 124);
d) Qual o valor de QI que a partir do qual temos os 16% menos pontuados?
Problema 3
Em um determinado país, o número médio mensal de suicídios é 2,75. Assumindo que o
número de suicídios segue uma distribuição de Poisson:
a) Qual a probabilidade de que nenhum suicídio seja registrado em um determinado mês?
b) Qual a probabilidade de que no máximo quatro suicídios sejam registrados?
c) Qual a probabilidade de que seis ou mais suicídios sejam registrados?
Problema 4
Suponha que, para uma certa população, os níveis de ácido úrico sejam normalmente
distribuídos com média 0,75 (g/24 horas) e desvio-padrão igual a 0,2 (g/24 horas). Estime a probabilidade de um indivíduo apresentar uma taxa de ácido úrico:
a) maior do que 1 (g/24 horas)
b) menor do que 0,8 (g/24 horas)
c) entre 0,85 e 1,15 (g/24 horas)
Problema 5
Suponha que o tempo de coagulação (TC) em seres humanos seja uma variável aleatória com distribuição normal, de média 7 minutos e desvio-padrão 1 minuto. Em um exame hematológico qualquer, determine a probabilidade de que um indivíduo apresente TC:
a) menor que 8 minutos
b) maior que 10 minutos
c) entre 4 e 10 minutos
quarta-feira, 7 de maio de 2008
A distribuição normal

A distribuição Normal é a mais familiar das distribuições de probabilidade e também uma das mais importantes em estatística. Esta distribuição tem uma forma de sino.
A equação da curva Normal é especificada usando 2 parâmetros: a média populacional , e o desvio padrão populacional , ou equivalentemente a variância populacional . Denotamos N() à curva Normal com média e variância . A média refere-se ao centro da distribuição e o desvio padrão ao espalhamento de curva. A distribuição normal é simétrica em torno da média o que implica que e média, a mediana e a moda são todas coincidentes. Para referência, a equação da curva é:
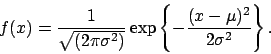

A área sob a curva normal (na verdade abaixo de qualquer função de densidade de probabilidade) é 1. Então, para quaisquer dois valores específicos podemos determinar a proporção de área sob a curva entre esses dois valores.
Na prática desejamos calcular probabilidades para diferentes valores de e . Para isso, a variável cuja distribuição é é transformada numa forma padronizada com distribuição (distribuição normal padrão) pois tal distribuição é tabelada. A quantidade é dada por

terça-feira, 6 de maio de 2008
Distribuição binomial

Definições
A distribuição binomial verifica as seguintes condições:
1. A experiência tem um nº fixo de provas, n.
2. As provas são independentes. (O resultado de uma
prova não afecta a probabilidade de ocorrência das
restantes.)
3. Cada prova origina um de dois resultados possíveis:
sucesso ou insucesso.
4. A probabilidade de sucesso, denotada por p, é
constante em cada prova.
Notação para a Distribuição Binomial
n denota o nº de provas (valor fixo à partida).
x denota um nº específico de sucessos em n
provas, logo x pode ser qualquer nº entre 0 e
n, inclusive.
p denota a probabilidade de sucesso em cada
uma das n provas.
q denota a probabilidade de insucesso em cada
uma das n provas.
P(x) denota a probabilidade de obter exactamente x
sucessos em n provas (P(x)=P(X=x)).
Fórmulas da Probabilidade na Distribuição Binomial
P(X=x)= [n!/x!(n-x)!].p^x.q^(n-x)
para x = 0, 1, 2, . . ., n
onde:
n = nº de provas
x = nº de sucessos nas n provas
p = probabilidade de sucesso em cada prova
q = probabilidade de insucesso em cada prova (q = 1 – p)
Média μ = n • p
Variância s^2 = n • p • q
Desvio Padrão s = n • p • q (raíz quadrada)
onde:
n = nº de provas
p = probabilidade de sucesso em cada uma das n
provas
q = probabilidade de insucesso em cada uma das n
provas
Distribuição Normal

Suponhamos que uma galinha de uma dada linhagem produz,num período de 72 semanas,300 ovos em média com um desvio-padrão de 5 ovos, e que esta variável (produção de ovos) apresenta distribuição aproximadamente Normal. Calcula a probabilidade de uma galinha dessa linhagem produzir, em 72 semanas, um número:
a) inferior a 290 ovos;
b) superior a 310 ovos;
c) entre 290 e 310 ovos.
resultados: 2,28% ; 2,28% ; 95,44%
segunda-feira, 25 de fevereiro de 2008
domingo, 24 de fevereiro de 2008
Probabilidade condicionada
Na matemática, a probabilidade condicionada refere-se à probabilidade de um evento A sabendo que ocorreu um outro evento B e representa-se por P(A|B).
Definição
A probabilidade de A condicionada por B (ou dado B, ou sabendo que B) é definida por:

Exemplo
Considere-se um baralho de 52 cartas. A probabilidade de ao retirar uma carta sair um rei é 4/52, ou 1/13. No entanto, se alguém retira uma carta e nos diz que é uma figura, então a probabilidade de ter saído um rei é 4/12=1/3, ou seja, P(sair um rei|sair uma figura)=1/3.
Acontecimentos independentes
Dois acontecimentos dizem-se independentes se:
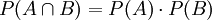
Isto significa que:

ou seja, que a ocorrência de B não tem qualquer efeito sobre a probabilidade de acontecer A.
Teorema de Bayes
O teorema de Bayes relaciona as probabilidade de A e B com as respectivas probabilidades condicionadas mútuas. Este teorema afirma que:

Falácia da probabilidade condicionada
A falácia da probabilidade condicionada consiste em supor que P(A|B) é igual a P(B|A). No entanto, pelo teorema de Bayes, estas probabilidades condicionadas só são iguais se A e B tiverem a mesma probabilidade.
Definição
A probabilidade de A condicionada por B (ou dado B, ou sabendo que B) é definida por:

Exemplo
Considere-se um baralho de 52 cartas. A probabilidade de ao retirar uma carta sair um rei é 4/52, ou 1/13. No entanto, se alguém retira uma carta e nos diz que é uma figura, então a probabilidade de ter saído um rei é 4/12=1/3, ou seja, P(sair um rei|sair uma figura)=1/3.
Acontecimentos independentes
Dois acontecimentos dizem-se independentes se:
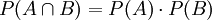
Isto significa que:

ou seja, que a ocorrência de B não tem qualquer efeito sobre a probabilidade de acontecer A.
Teorema de Bayes
O teorema de Bayes relaciona as probabilidade de A e B com as respectivas probabilidades condicionadas mútuas. Este teorema afirma que:

Falácia da probabilidade condicionada
A falácia da probabilidade condicionada consiste em supor que P(A|B) é igual a P(B|A). No entanto, pelo teorema de Bayes, estas probabilidades condicionadas só são iguais se A e B tiverem a mesma probabilidade.
O Problema de Monty-Hall
O problema de Monty Hall ou paradoxo de Monty Hall é um problema matemático e paradoxo que surgiu a partir de um concurso televisivo dos Estados Unidos da América chamado Let’s Make a Deal, exibido na década de 1970.
O jogo consiste no seguinte: Monty Hall (o apresentador) apresentava 3 portas aos concorrentes, sabendo que atrás de uma delas está um carro (prémio bom) e que as outras têm prêmios de pouco valor.

Na 1ª etapa o concorrente escolhe uma porta (que ainda não é aberta);
De seguida Monty abre uma das outras duas portas que o concorrente não escolheu, sabendo à partida que o carro não se encontra aí;
Agora com duas portas apenas para escolher -- pois uma delas já se viu, na 2ª etapa, que não tinha o prêmio -- e sabendo que o carro está atrás de uma delas, o concorrente tem que se decidir se permanece com a porta que escolheu no início do jogo e abre-a ou se muda para a outra porta que ainda está fechada para então a abrir.
Qual é a estratégia mais lógica? Ficar com a porta escolhida inicialmente ou mudar de porta? Com qual das duas portas ainda fechadas o concorrente tem mais probabilidades de ganhar? Porquê?
solução do problema
Uma primeira análise poderia levar a pensar que não, porque nas duas restantes portas a probabilidade de se ganhar o carro, tendo sido eliminada uma das portas, seria de 50 % para cada uma das duas restantes. Parece inútil trocar.
Mas a realidade é que trocar de porta duplica a probabilidade de ganhar o carro ! Com efeito, à partida, as probabilidades de se ganhar o carro na porta escolhida e nas duas restantes portas são 1/3 e 2/3, respectivamente. Mas não se sabe qual das duas portas não escolhidas conterá o carro e apenas se pode escolher uma única porta.
Ao ser revelado o conteúdo de uma destas duas portas, a probabilidade do prémio estar contido em ambas mantém-se igualmente em 2/3 mas agora sabe-se que a probabilidade de estar na porta revelada é igual a 0. Logo, estes 2/3 de hipótese de ganho estarão contidos integralmente na porta por abrir, que o concorrente não escolheu à partida mas que pode escolher se optar por trocar a sua opção inicial. A conclusão a tirar é que vale a pena trocar de porta porque assim se duplica a probabilidade inicial de ganhar o carro !
Este problema, por ser pouco intuitivo para a maior parte das pessoas, confundiu muita gente, inclusivamente ilustres matemáticos, na altura em que foi colocado (excepto a mulher com o maior QI do mundo, que o resolveu à primeira). É um facto que muitos deles apenas ficaram convencidos da solução após executarem uma simulação em computador para verificarem experimentalmente os referidos 2/3 de probabilidade.
O jogo consiste no seguinte: Monty Hall (o apresentador) apresentava 3 portas aos concorrentes, sabendo que atrás de uma delas está um carro (prémio bom) e que as outras têm prêmios de pouco valor.

Na 1ª etapa o concorrente escolhe uma porta (que ainda não é aberta);
De seguida Monty abre uma das outras duas portas que o concorrente não escolheu, sabendo à partida que o carro não se encontra aí;
Agora com duas portas apenas para escolher -- pois uma delas já se viu, na 2ª etapa, que não tinha o prêmio -- e sabendo que o carro está atrás de uma delas, o concorrente tem que se decidir se permanece com a porta que escolheu no início do jogo e abre-a ou se muda para a outra porta que ainda está fechada para então a abrir.
Qual é a estratégia mais lógica? Ficar com a porta escolhida inicialmente ou mudar de porta? Com qual das duas portas ainda fechadas o concorrente tem mais probabilidades de ganhar? Porquê?
solução do problema
Uma primeira análise poderia levar a pensar que não, porque nas duas restantes portas a probabilidade de se ganhar o carro, tendo sido eliminada uma das portas, seria de 50 % para cada uma das duas restantes. Parece inútil trocar.
Mas a realidade é que trocar de porta duplica a probabilidade de ganhar o carro ! Com efeito, à partida, as probabilidades de se ganhar o carro na porta escolhida e nas duas restantes portas são 1/3 e 2/3, respectivamente. Mas não se sabe qual das duas portas não escolhidas conterá o carro e apenas se pode escolher uma única porta.
Ao ser revelado o conteúdo de uma destas duas portas, a probabilidade do prémio estar contido em ambas mantém-se igualmente em 2/3 mas agora sabe-se que a probabilidade de estar na porta revelada é igual a 0. Logo, estes 2/3 de hipótese de ganho estarão contidos integralmente na porta por abrir, que o concorrente não escolheu à partida mas que pode escolher se optar por trocar a sua opção inicial. A conclusão a tirar é que vale a pena trocar de porta porque assim se duplica a probabilidade inicial de ganhar o carro !
Este problema, por ser pouco intuitivo para a maior parte das pessoas, confundiu muita gente, inclusivamente ilustres matemáticos, na altura em que foi colocado (excepto a mulher com o maior QI do mundo, que o resolveu à primeira). É um facto que muitos deles apenas ficaram convencidos da solução após executarem uma simulação em computador para verificarem experimentalmente os referidos 2/3 de probabilidade.
terça-feira, 19 de fevereiro de 2008
Dois votos: o sistema eleitoral alemão

No fundo, é tudo muito simples: com o seu "x" no boletim de voto, os alemães decidem quem terá um mandato no Parlamento e quem ficará de fora. Mas, então, que papel representam a cláusula dos cinco por cento, os mandatos suplementares, o primeiro e o segundo votos no resultado final da eleição?
Na Alemanha, o voto não é obrigatório e, sim, facultativo. Para determinar a composição do Bundestag –num total de 598 mandatos – cada eleitor tem direito a dois votos.
O segundo voto é decisivo
Com seu primeiro voto, os eleitores escolhem o deputado que deverá representar o seu distrito eleitoral em Berlim. É o chamado "mandato directo". A maioria simples dos votos decide a obtenção do mandato em cada distrito eleitoral.Metade do número de deputados (ou seja, 299) é escohida desta maneira.
A formação das maiorias parlamentares, contudo, depende fundamentalmente do segundo voto – um voto de legenda. Com ele, os eleitores escolhem os ocupantes das 299 cadeiras parlamentares restantes e determinam também a força política de cada um dos partidos.
Lista eleitoral
Os partidos estabelecem, em cada Estado, uma lista eleitoral hierárquica com os nomes dos candidatos a serem enviados como deputados a Berlim de acordo com o número obtido de votos de legenda.
A grande importância do segundo voto decorre do facto de ser ele determinante para o número total de deputados de um partido. O total dos mandatos parlamentares é distribuído entre os partidos segundo a proporção dos respectivos votos de legenda. Deduz-se, porém, o número de mandatos directos conquistados.
Um exemplo: após o apuramento final dos votos de legenda, cabe a um determinado partido um total de 100 mandatos. Mas o partido conquistou 40 mandatos directos – os outros 60 deputados sairão, por ordem hierárquica, da lista de candidatos. Se o mesmo partido só tiver conquistado 30 mandatos directos, os 70 primeiros nomes da lista partidária serão enviados então a Berlim como deputados.
Mandatos suplementares
Até aqui, o que foi citado é a regra geral. Mas existe também um caso especial – o dos mandatos suplementares. Isto ocorre quando um partido conquista mandatos directos em número superior ao total a que teria direito de acordo com os votos de legenda obtidos.
O partido pode, então, ficar com tais mandatos excedentes, aumentando assim o número total dos deputados ao Parlamento federal alemão. Em 1994, houve um total de 16 mandatos suplementares. Nas eleições federais de 1998, o número foi um pouco menor: 13 mandatos. Na última eleição, em 2002, esse número caiu para cinco.
Cinco por cento é o mínimo
O sistema eleitoral alemão tem ainda um regulamento peculiar: a cláusula dos cinco por cento. Segundo ela, qualquer partido só obtém representação no Parlamento se obtiver um mínimo de 5% do total de votos de legenda. Isto evita que um número infindável de partidos de pequena expressão se façam representar no Bundestag, com conseqüências negativas para um trabalho parlamentar eficaz.
Mas, como todas as regras, também esta tem uma excepção. Se um partido não consegue obter 5% dos votos de legenda, mas conquista três ou mais mandatos directos, então tem o direito de se fazer representar no Parlamento. Neste caso, os seus votos de legenda são tomados como base de cálculo para o seu número total de mandatos.
domingo, 17 de fevereiro de 2008
Os algoritmos do bolo-rei
Todos conhecemos a melhor maneira de repartir um bolo entre duas pessoas, sem que nenhuma se possa queixar: uma parte e outra escolhe. O problema complica-se quando há mais de dois parceiros. Por muito trivial que pareça, os matemáticos têm tratado este problema, obtendo algoritmos de repartição eficazes.


Texto de Nuno Crato
«Quem parte e reparte, e não fica com a melhor parte, ou é tolo ou não tem arte», diz um ditado popular. É verdade: se a pessoa a fazer a divisão for também a que fizer a escolha, nada garante que um dos parceiros não fique prejudicado. Por isso, e para evitar que alguém se possa queixar do resultado da partilha, o melhor é proceder em duas etapas: um dos parceiros divide o bolo e o outro escolhe a sua fatia.
Desta forma, é do interesse do primeiro fazer a divisão da forma mais equitativa possível, pois se assim não acontecer, terá a certeza de ficar com o pior bocado. É uma sábia conjugação de situações, pois os dois parceiros, afinal ambos movidos pelo egoísmo, colaboram de forma a que nenhum fique prejudicado.
A história é muito conhecida e aplicada em várias situações do dia-a-dia, e não só na divisão de guloseimas entre crianças. O problema complica-se, contudo, se o bolo tiver de ser dividido entre mais do que dois parceiros. Como é que se há-de fazer se forem três, por exemplo? Ou se forem muito mais? E se tivermos um bolo-rei a dividir entre 20 pessoas igualmente gulosas?
O problema não é simples e os matemáticos têm vindo a desenvolver algoritmos para partilhas equitativas. Esses algoritmos, isto é, esses procedimentos sistemáticos de busca de uma solução, podem ter aplicações em áreas muito diversas, desde a partilha de heranças e divisão de obrigações pecuniárias até às negociações de desarmamento ou ao estabelecimento de fronteiras entre países.
O algoritmo «um parte, outro escolhe» pode aplicar-se a mais do que dois parceiros. Se tivermos quatro pretendentes a um bolo-rei, por exemplo, o algoritmo desdobra-se em duas etapas. Começam-se por agrupar os pretendentes ao bolo em dois grupos, com dois elementos em cada grupo. Um dos grupos divide o bolo em duas partes e o outro escolhe a sua metade. Na segunda etapa, cada par de gulosos divide a sua metade de bolo-rei ao meio, seguindo de novo o processo de um partir e o outro escolher.
É fácil ver que este método pode funcionar igualmente para oito pessoas ou, em geral, para potências de dois. Mas já não é tão simples encontrar uma solução no caso de haver três pessoas. Pensando bem, consegue-se arranjar um método que funcione nesse caso. Quer o leitor dar uma sugestão?
Os matemáticos, contudo, não gostam de soluções que apenas funcionam para casos particulares, pelo que têm procurado algoritmos mais gerais. O ideal seria encontrar um método que funcionasse com qualquer número de pessoas. Um desses métodos, proposto pelos matemáticos polacos Stefan Banach (1892-1945) e Bronislaw Knaster (1893-1980), resolve o problema com qualquer número de parceiros. É o chamado algoritmo da faca deslizante. Este caso é mais fácil de perceber com um bolo sobre o comprido, como um bolo inglês.
Os diversos pretendentes às fatias do bolo reúnem-se à sua volta enquanto uma pessoa, possivelmente um deles, pouco importa, começa a deslizar a faca sobre o bolo, a partir de um dos lados. Vai-se progredindo com a faca até que um dos parceiros diga «Pára!». Nesse momento, pára-se a faca e corta-se uma fatia, que é entregue a quem falou. O parceiro em causa fica assim com uma parte que considera ser, pelo menos, uma fracção justa do bolo - se pensasse que a faca não tinha ainda chegado a essa fracção justa, não a teria reclamado. Os outros, por seu lado, vêem o bolo ser diminuído do que consideram ser inferior ou igual a uma fracção justa - se algum deles achasse que a faca tinha já ultrapassado o momento certo, deveria ter reclamado a fatia correspondente.
Depois de o primeiro parceiro ter recolhido a sua fatia, este afasta-se do jogo, enquanto a faca continua a deslizar, até que um dos restantes parceiros diga «Pára» e recolha a sua fatia. O processo repete-se até restarem apenas dois parceiros. Nessa altura, o primeiro a falar é o que fica com a fatia reclamada e o último fica com o restante. O interessante neste processo é que, mesmo admitindo a falibilidade de cada uma das pessoas, nenhuma delas pode reclamar que está a ser prejudicada. Se o está, é por sua culpa, pois não terá falado a tempo, ou terá falado cedo demais, sem a isso ninguém a ter obrigado.
Este método parece perfeito, mas deixa de fora alguns casos interessantes. Funciona para um bolo homogéneo, mas funcionará para um bolo com constituintes diversos e irregularmente distribuídos, como é o caso do bolo-rei? Será possível arranjar um algoritmo em que todos fiquem com igual quantidade de abóbora cristalizada, de pinhões, de passas e de massa? A resposta a esta questão foi dada por um teorema que o matemático polaco Hugo Steinhaus (1887-1972) demonstrou nos anos 40 e que veio a ser conhecido pelo curioso nome de Teorema da Sanduíche de Fiambre. Considere-se um objecto tridimensional com três componentes, por exemplo, uma sanduíche com pão, queijo e fiambre - pouco importa que esses componentes estejam bem ou mal distribuídos, que se concentrem em lados diferentes ou que estejam uniformemente espalhados. O que esse resultado prova é que há sempre um plano que divide o objecto em duas partes, de tal maneira que cada uma delas contenha igual quantidade dos três componentes. Ou seja, mesmo que o fiambre e o queijo estejam mal espalhados, há sempre uma maneira de cortar a sanduíche em dois bocados rigorosamente iguais.
Quando se considera um objecto bidimensional, já a partição equitativa apenas funciona com dois componentes. Suponha-se que se espalha sal e pimenta numa mesa, por exemplo. O teorema de Steinhaus mostra que há sempre uma recta que divide a superfície da mesa em duas partes que têm iguais quantidades de sal e de pimenta. Se houver três ingredientes, suponhamos sal, pimenta e açúcar, é fácil de imaginar uma concentração em três locais diferentes de tal forma que não haja linha recta que faça a partição de forma equitativa. De forma geral, o teorema diz que em «n» dimensões há sempre um hiperplano que divide simultaneamente ao meio «n» componentes. Como parece que vivemos a três dimensões e o bolo-rei tem muito mais que três constituintes, ficamos a saber: não há faca que os reparta todos equitativamente.


Texto de Nuno Crato
«Quem parte e reparte, e não fica com a melhor parte, ou é tolo ou não tem arte», diz um ditado popular. É verdade: se a pessoa a fazer a divisão for também a que fizer a escolha, nada garante que um dos parceiros não fique prejudicado. Por isso, e para evitar que alguém se possa queixar do resultado da partilha, o melhor é proceder em duas etapas: um dos parceiros divide o bolo e o outro escolhe a sua fatia.
Desta forma, é do interesse do primeiro fazer a divisão da forma mais equitativa possível, pois se assim não acontecer, terá a certeza de ficar com o pior bocado. É uma sábia conjugação de situações, pois os dois parceiros, afinal ambos movidos pelo egoísmo, colaboram de forma a que nenhum fique prejudicado.
A história é muito conhecida e aplicada em várias situações do dia-a-dia, e não só na divisão de guloseimas entre crianças. O problema complica-se, contudo, se o bolo tiver de ser dividido entre mais do que dois parceiros. Como é que se há-de fazer se forem três, por exemplo? Ou se forem muito mais? E se tivermos um bolo-rei a dividir entre 20 pessoas igualmente gulosas?
O problema não é simples e os matemáticos têm vindo a desenvolver algoritmos para partilhas equitativas. Esses algoritmos, isto é, esses procedimentos sistemáticos de busca de uma solução, podem ter aplicações em áreas muito diversas, desde a partilha de heranças e divisão de obrigações pecuniárias até às negociações de desarmamento ou ao estabelecimento de fronteiras entre países.
O algoritmo «um parte, outro escolhe» pode aplicar-se a mais do que dois parceiros. Se tivermos quatro pretendentes a um bolo-rei, por exemplo, o algoritmo desdobra-se em duas etapas. Começam-se por agrupar os pretendentes ao bolo em dois grupos, com dois elementos em cada grupo. Um dos grupos divide o bolo em duas partes e o outro escolhe a sua metade. Na segunda etapa, cada par de gulosos divide a sua metade de bolo-rei ao meio, seguindo de novo o processo de um partir e o outro escolher.
É fácil ver que este método pode funcionar igualmente para oito pessoas ou, em geral, para potências de dois. Mas já não é tão simples encontrar uma solução no caso de haver três pessoas. Pensando bem, consegue-se arranjar um método que funcione nesse caso. Quer o leitor dar uma sugestão?
Os matemáticos, contudo, não gostam de soluções que apenas funcionam para casos particulares, pelo que têm procurado algoritmos mais gerais. O ideal seria encontrar um método que funcionasse com qualquer número de pessoas. Um desses métodos, proposto pelos matemáticos polacos Stefan Banach (1892-1945) e Bronislaw Knaster (1893-1980), resolve o problema com qualquer número de parceiros. É o chamado algoritmo da faca deslizante. Este caso é mais fácil de perceber com um bolo sobre o comprido, como um bolo inglês.
Os diversos pretendentes às fatias do bolo reúnem-se à sua volta enquanto uma pessoa, possivelmente um deles, pouco importa, começa a deslizar a faca sobre o bolo, a partir de um dos lados. Vai-se progredindo com a faca até que um dos parceiros diga «Pára!». Nesse momento, pára-se a faca e corta-se uma fatia, que é entregue a quem falou. O parceiro em causa fica assim com uma parte que considera ser, pelo menos, uma fracção justa do bolo - se pensasse que a faca não tinha ainda chegado a essa fracção justa, não a teria reclamado. Os outros, por seu lado, vêem o bolo ser diminuído do que consideram ser inferior ou igual a uma fracção justa - se algum deles achasse que a faca tinha já ultrapassado o momento certo, deveria ter reclamado a fatia correspondente.
Depois de o primeiro parceiro ter recolhido a sua fatia, este afasta-se do jogo, enquanto a faca continua a deslizar, até que um dos restantes parceiros diga «Pára» e recolha a sua fatia. O processo repete-se até restarem apenas dois parceiros. Nessa altura, o primeiro a falar é o que fica com a fatia reclamada e o último fica com o restante. O interessante neste processo é que, mesmo admitindo a falibilidade de cada uma das pessoas, nenhuma delas pode reclamar que está a ser prejudicada. Se o está, é por sua culpa, pois não terá falado a tempo, ou terá falado cedo demais, sem a isso ninguém a ter obrigado.
Este método parece perfeito, mas deixa de fora alguns casos interessantes. Funciona para um bolo homogéneo, mas funcionará para um bolo com constituintes diversos e irregularmente distribuídos, como é o caso do bolo-rei? Será possível arranjar um algoritmo em que todos fiquem com igual quantidade de abóbora cristalizada, de pinhões, de passas e de massa? A resposta a esta questão foi dada por um teorema que o matemático polaco Hugo Steinhaus (1887-1972) demonstrou nos anos 40 e que veio a ser conhecido pelo curioso nome de Teorema da Sanduíche de Fiambre. Considere-se um objecto tridimensional com três componentes, por exemplo, uma sanduíche com pão, queijo e fiambre - pouco importa que esses componentes estejam bem ou mal distribuídos, que se concentrem em lados diferentes ou que estejam uniformemente espalhados. O que esse resultado prova é que há sempre um plano que divide o objecto em duas partes, de tal maneira que cada uma delas contenha igual quantidade dos três componentes. Ou seja, mesmo que o fiambre e o queijo estejam mal espalhados, há sempre uma maneira de cortar a sanduíche em dois bocados rigorosamente iguais.
Quando se considera um objecto bidimensional, já a partição equitativa apenas funciona com dois componentes. Suponha-se que se espalha sal e pimenta numa mesa, por exemplo. O teorema de Steinhaus mostra que há sempre uma recta que divide a superfície da mesa em duas partes que têm iguais quantidades de sal e de pimenta. Se houver três ingredientes, suponhamos sal, pimenta e açúcar, é fácil de imaginar uma concentração em três locais diferentes de tal forma que não haja linha recta que faça a partição de forma equitativa. De forma geral, o teorema diz que em «n» dimensões há sempre um hiperplano que divide simultaneamente ao meio «n» componentes. Como parece que vivemos a três dimensões e o bolo-rei tem muito mais que três constituintes, ficamos a saber: não há faca que os reparta todos equitativamente.
sábado, 16 de fevereiro de 2008
O Teorema das Quatro Cores

O teorema do mapa de quatro cores diz que não são necessárias mais de quatro cores para pintar qualquer mapa plano concebível, de países reais ou imaginário, de tal modo que dois países vizinhos não tenham a mesma cor.
A demonstração deste teorema é considerado um dos maiores feitos da matemática moderna. Este foi um dos primeiros grandes teoremas a ser provado usando um computador, no entanto esta prova não é ainda aceite por todos os matemáticos visto ninguém o ter conseguido demonstrar usando apenas papel e caneta.
Em meado do século XIX os matemáticos pensavam que este teorema era verdadeiro, tendo sido proposto como conjectura em 1852 por Francis Guthrie, que se apercebeu enquanto pintava o mapa dos condado de Inglaterra que apenas necessitava de quatro cores. Durante mais de 100 anos matemáticos de todo o mundo atacaram o problema com unhas e dentes tendo sempre falhado na sua demonstração.
No livro O Homem Que Só Gostava de Números, Paul Hoffman conta a história de um matemático, chamado E.F. Moore, que teve durante uns tempos como objectivo de vida encontrar um contra exemplo. Todos os dias chegava ao trabalho, na AT&M, com uma folha gigante de papel com mais de um metro quadrado onde tinha cuidadosamente desenhado um mapa com milhares de países. "Hoje vou conseguir", dizia ele pela manhã, "vou provar que são precisas 5 cores". Ao fim do dia saía desiludido. Mas na manhã seguinte lá estava ele com um lençol cheio de minúsculos e intrincados países imaginários.
Foi apenas em 1976 que a conjectura foi finalmente demonstrada por Kenneth Appel e Wolfgang Haken na Universidade de Illinois. Quando isto aconteceu reza a história que muitos professores de matemática terão interrompido as sua aulas para abrir uma garrafa de champanhe. No entanto muitos matemáticos não ficaram contentes, pois a descoberta tinha sido feita usando 3 supercomputadores durante mais de 1000 horas. Na realidade Appel e Haken demonstraram que todos os mapas possíveis eram variações de 1500 tipos fundamentais, e os computadores conseguiram pintá-los a todos com um máximo de quatro cores. Há quem acredite ainda que este teorema pode ser demonstrado com papel, lápis e umas poucas folhas.

Bibliografia:
- Four color theorem, Wikipédia
- O Homem Que Só Gostava de Números, Ciência Aberta, Nº105, Gradiva.
sábado, 26 de janeiro de 2008
Paradoxos Eleitorais


Expresso – Março/2002
MATEMÁTICA
Paradoxos eleitorais - um texto de Nuno Crato
O estudo matemático dos sistemas eleitorais mostra que não há sistema perfeito e que as eleições são muitas vezes decididas pelo voto dos que não apoiam o candidato vencedor.
O voto é uma das grandes conquistas da Humanidade. Ainda nada melhor foi inventado para conseguir um sistema de governo que garanta a liberdade e o progresso. E será possível inventá-lo?
O sistema usado nas democracias baseia-se no chamado voto plural, que é mais conhecido pela sigla «Um homem um voto». Aqui, «homem» representa cidadão, portanto admitimos que o voto plural inclui homens e mulheres. Parece um sistema justo. E é. Mas não está isento de paradoxos, de situações aparentemente contraditórias e surpreendentes que têm sido notadas desde a Antiguidade.
Ao que se sabe, terá sido Plínio, o Novo, assim chamado para o distinguir do tio, Plínio, o Velho, quem primeiro revelou algumas situações paradoxais
derivadas do voto. Estava-se no século II d.C. e as eleições estavam reservadas a uma elite, mas os problemas eram os mesmos. No século XVII, os paradoxos eleitorais começaram a ser discutidos sistematicamente. Procurava-se um sistema de eleições perfeito e racional e começaram a surgir os problemas.
O matemático francês Jean-Charles Borda (1733-1799) foi o primeiro a estudar sistematicamente o problema. O que descobriu surpreendeu os seus contemporâneos. Olhando para o sistema eleitoral como um método de agregar opiniões para encontrar uma escolha colectiva, notou que métodos diferentes conduzem a resultados diferentes. O paradoxo de Borda, como veio a ser conhecido, foi muito discutido na época, sem se encontrar uma solução satisfatória.
Borda apresentou o problema à Academia Real Francesa em 16 de Junho de 1770. Colocou um exemplo em que 21 votantes escolhiam entre 3 candidatos. Considerou as preferências relativas de cada votante, isto é a forma como cada eleitor
hierarquizava os candidatos. O que reparou foi que era possível eleger um candidato que a maioria dos eleitores colocava em último lugar. O que reparou foi que era possível eleger um candidato que a maioria dos eleitores colocava em último lugar. Bastava para isso que os votos dos outros dois estivessem suficientemente divididos. Modernamente chama-se a isso a eleição de um perdedor de Condorcet, isto é, de um candidato que perde em comparações bilaterais com todos os outros. No exemplo de Borda, o candidato A perdia as eleições se apenas as disputasse com o candidato B, perdê-las-ia de novo se apenas se defrontasse com o candidato C, mas ganhá-las-ia se fosse às urnas contra os dois em simultâneo.
Para resolver o paradoxo, Borda propôs um sistema que veio a ser chamado contagem de Borda. É semelhante ao que é aplicado no Festival da Canção e em outros concursos. Em vez do sistema «um homem um voto», Borda dava a cada eleitor a possibilidade de atribuir uma pontuação a cada candidato. Havendo três, cada eleitor daria dois pontos ao candidato que preferisse, um ponto ao da sua segunda preferência e zero ao restante. Os pontos seriam depois somados e a escolha recairia sobre o candidato mais pontuado.
O sistema parece perfeito, mas tem também os seus problemas. Primeiramente, por que razão tem a preferência que ser linear? Dar-se zero pontos ao candidato menos querido, um ponto ao seguinte e por aí adiante, pode não reflectir exactamente as nossas preferências. Não poderia um votante dar zero pontos a um candidato, meio ponto ao seguinte e ponto e meio a um terceiro? O curioso é que, se assim fosse, o vencedor poderia não ser o mesmo. Com idênticas ordenações das preferências, o candidato mais votado pode depender dos pesos que se fixarem. Quer dizer, o sistema de pontos nem sempre dá o mesmo resultado. Este sistema de eleições também permite graus de arbitrariedade.
Mais grave ainda, como o mostrou um compatriota de Borda, o matemático e filósofo Marquês de Condorcet (1743-94), nem sempre é possível agregar as preferências dos votantes de forma coerente. As preferências de cada eleitor devem ter uma propriedade elementar, devem ser transitivas: se um eleitor põe o candidato A à frente do B e coloca o B à frente do C, então também colocará o A adiante do C.
Numa colectividade e em eleições em que haja pelo menos três candidatos, não é isso que se passa. A colectividade pode preferir A a B, preferir B a C e, no entanto, preferir C a A! Como se resolverá este problema?
Donald Saari, um matemático da Universidade de Califórnia em Irvine que se tem dedicado a estudar os problemas eleitorais, mostrou que pequenas mudanças em qualquer sistema eleitoral podem trazer grandes alterações nos resultados das eleições. Saari é um dos matemáticos e especialistas de ciência política que se têm dedicado a estudar os problemas da chamada escolha pública, uma área que sofreu um grande desenvolvimento na segunda metade do século XX.
Nesta altura, o leitor pode já suspeitar que seja difícil encontrar um sistema perfeito. Mas o problema é ainda mais complexo do que à primeira vista parece. Kenneth J. Arrow, um matemático e economista norte-americano que recebeu o prémio Nobel em 1972, estudou um conjunto de condições eleitorais aparentemente razoáveis, tais como a discutida transitividade das preferências, e mostrou que não há nenhum sistema eleitoral democrático que satisfaça simultaneamente todas essas condições.
Que se pode então fazer? Matematicamente o problema não tem solução, mas a sociedade não precisa de sistemas perfeitos e sim de regras falíveis e aproximadas, que conduzam a escolhas colectivamente aceites. A matemática pode ajudar a perceber os problemas dos diversos sistemas eleitorais. Mas não põe em causa a democracia, pois essa é uma escolha moral colectiva que a História tem revelado ser acertada.
NÃO HÁ SOLUÇÕES PERFEITAS
Segundo o paradoxo de Jean-Charles Borda (ver tabela I), cada perfil de preferências corresponde a uma coluna, que tem o número de votantes indicado. Assim, por exemplo, apenas uma pessoa coloca o candidato A em primeiro lugar, seguido do B e, depois, do C. Na segunda coluna vemos que há 7 votantes que preferem o candidato A, que põem em segundo lugar o candidato C e em terceiro o B. Neste exemplo de Borda, o candidato mais votado segundo o sistema plural (um homem um voto) é A, com 8 votos a favor, contra 7 em B e 6 em C. No entanto, esse é o candidato mais detestado pela maioria do eleitorado, uma vez que 13 votantes em 21 o colocam em último lugar.
O paradoxo de Condorcet (ver tabela II) é igualmente intrigante. Suponhamos que os votantes estão divididos em três grupos com as preferências da segunda tabela: Para o primeiro grupo de votantes, o candidato A é o preferido, seguido do B e, depois, do C. Há uma lógica transitiva nas escolhas deste grupo. Se se prefere A a B e se prefere B a C, então também se prefere A a C. Mas essa transitividade não se transporta para o conjunto de votantes. Suponhamos que há um número idêntico de votantes em cada grupo. Então, A vence B, pois é essa a hierarquia que tanto o grupo 1 como o 3 estabelecem. É essa a opinião da maioria dos votantes. Por outro lado, B também vence C, pois essa é a hierarquia que tanto o grupo 1 como o 2 definem. Pareceria lógico que A vencendo B e B vencendo C, então A também teria de vencer C. No entanto, C vence A, como se pode ver pelo mesmo raciocínio: tanto o grupo 2 como o 3 colocam C antes de A.
Paradoxo de Borda (tabela I)
1ª escolha/2ª escolha/3ª escolha
A, B, C - 1 votante
A, C, B - 7 votantes
B, C, A - 7 votantes
C, B, A - 6 votantes
Paradoxo de Condorcet (tabela II)
1ª escolha/2ª escolha/3ª escolha
A, C, B - Grupo 1
B, C, A - Grupo 2
C, A, B - Grupo 3
quarta-feira, 23 de janeiro de 2008
sexta-feira, 18 de janeiro de 2008
MACS (Bloco I) - Programação
- Modelação Matemática (Teoria Matemática das Eleições / Teoria da Partilha Equilibrada)
- Estatística Descritiva
- Modelação Financeira
Programação de MACS - Bloco II
- Modelos Matemáticos ( Teoria de Grafos / Modelos Populacionais)
- Modelos de Probabilidades
- Inferência Estatística
Subscrever:
Mensagens (Atom)
AS CLASSES DE GINÁSTICA - o método de Hamilton
Três classes de ginástica de um clube decidem constituir uma associação que defenda os seus interesses. A assembleia será constituída por 2...

-
Num grafo, chama-se circuito de Hamilton a um caminho que começa e acaba no mesmo vértice, passando por todos os vértices uma única vez. Alg...
-
Grafo - estrutura matemática usada para representar as relações entre as coisas ou objectos. Os grafos possuem nós ou vértices (coisas/ob...
-
Tabela para cálculo do IMT em 2008, aplicável no Continente É calculado multiplicando a "Taxa Marginal" pelo valor de transacção d...


