segunda-feira, 25 de fevereiro de 2008
domingo, 24 de fevereiro de 2008
Probabilidade condicionada
Na matemática, a probabilidade condicionada refere-se à probabilidade de um evento A sabendo que ocorreu um outro evento B e representa-se por P(A|B).
Definição
A probabilidade de A condicionada por B (ou dado B, ou sabendo que B) é definida por:

Exemplo
Considere-se um baralho de 52 cartas. A probabilidade de ao retirar uma carta sair um rei é 4/52, ou 1/13. No entanto, se alguém retira uma carta e nos diz que é uma figura, então a probabilidade de ter saído um rei é 4/12=1/3, ou seja, P(sair um rei|sair uma figura)=1/3.
Acontecimentos independentes
Dois acontecimentos dizem-se independentes se:
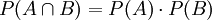
Isto significa que:

ou seja, que a ocorrência de B não tem qualquer efeito sobre a probabilidade de acontecer A.
Teorema de Bayes
O teorema de Bayes relaciona as probabilidade de A e B com as respectivas probabilidades condicionadas mútuas. Este teorema afirma que:

Falácia da probabilidade condicionada
A falácia da probabilidade condicionada consiste em supor que P(A|B) é igual a P(B|A). No entanto, pelo teorema de Bayes, estas probabilidades condicionadas só são iguais se A e B tiverem a mesma probabilidade.
Definição
A probabilidade de A condicionada por B (ou dado B, ou sabendo que B) é definida por:

Exemplo
Considere-se um baralho de 52 cartas. A probabilidade de ao retirar uma carta sair um rei é 4/52, ou 1/13. No entanto, se alguém retira uma carta e nos diz que é uma figura, então a probabilidade de ter saído um rei é 4/12=1/3, ou seja, P(sair um rei|sair uma figura)=1/3.
Acontecimentos independentes
Dois acontecimentos dizem-se independentes se:
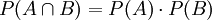
Isto significa que:

ou seja, que a ocorrência de B não tem qualquer efeito sobre a probabilidade de acontecer A.
Teorema de Bayes
O teorema de Bayes relaciona as probabilidade de A e B com as respectivas probabilidades condicionadas mútuas. Este teorema afirma que:

Falácia da probabilidade condicionada
A falácia da probabilidade condicionada consiste em supor que P(A|B) é igual a P(B|A). No entanto, pelo teorema de Bayes, estas probabilidades condicionadas só são iguais se A e B tiverem a mesma probabilidade.
O Problema de Monty-Hall
O problema de Monty Hall ou paradoxo de Monty Hall é um problema matemático e paradoxo que surgiu a partir de um concurso televisivo dos Estados Unidos da América chamado Let’s Make a Deal, exibido na década de 1970.
O jogo consiste no seguinte: Monty Hall (o apresentador) apresentava 3 portas aos concorrentes, sabendo que atrás de uma delas está um carro (prémio bom) e que as outras têm prêmios de pouco valor.

Na 1ª etapa o concorrente escolhe uma porta (que ainda não é aberta);
De seguida Monty abre uma das outras duas portas que o concorrente não escolheu, sabendo à partida que o carro não se encontra aí;
Agora com duas portas apenas para escolher -- pois uma delas já se viu, na 2ª etapa, que não tinha o prêmio -- e sabendo que o carro está atrás de uma delas, o concorrente tem que se decidir se permanece com a porta que escolheu no início do jogo e abre-a ou se muda para a outra porta que ainda está fechada para então a abrir.
Qual é a estratégia mais lógica? Ficar com a porta escolhida inicialmente ou mudar de porta? Com qual das duas portas ainda fechadas o concorrente tem mais probabilidades de ganhar? Porquê?
solução do problema
Uma primeira análise poderia levar a pensar que não, porque nas duas restantes portas a probabilidade de se ganhar o carro, tendo sido eliminada uma das portas, seria de 50 % para cada uma das duas restantes. Parece inútil trocar.
Mas a realidade é que trocar de porta duplica a probabilidade de ganhar o carro ! Com efeito, à partida, as probabilidades de se ganhar o carro na porta escolhida e nas duas restantes portas são 1/3 e 2/3, respectivamente. Mas não se sabe qual das duas portas não escolhidas conterá o carro e apenas se pode escolher uma única porta.
Ao ser revelado o conteúdo de uma destas duas portas, a probabilidade do prémio estar contido em ambas mantém-se igualmente em 2/3 mas agora sabe-se que a probabilidade de estar na porta revelada é igual a 0. Logo, estes 2/3 de hipótese de ganho estarão contidos integralmente na porta por abrir, que o concorrente não escolheu à partida mas que pode escolher se optar por trocar a sua opção inicial. A conclusão a tirar é que vale a pena trocar de porta porque assim se duplica a probabilidade inicial de ganhar o carro !
Este problema, por ser pouco intuitivo para a maior parte das pessoas, confundiu muita gente, inclusivamente ilustres matemáticos, na altura em que foi colocado (excepto a mulher com o maior QI do mundo, que o resolveu à primeira). É um facto que muitos deles apenas ficaram convencidos da solução após executarem uma simulação em computador para verificarem experimentalmente os referidos 2/3 de probabilidade.
O jogo consiste no seguinte: Monty Hall (o apresentador) apresentava 3 portas aos concorrentes, sabendo que atrás de uma delas está um carro (prémio bom) e que as outras têm prêmios de pouco valor.

Na 1ª etapa o concorrente escolhe uma porta (que ainda não é aberta);
De seguida Monty abre uma das outras duas portas que o concorrente não escolheu, sabendo à partida que o carro não se encontra aí;
Agora com duas portas apenas para escolher -- pois uma delas já se viu, na 2ª etapa, que não tinha o prêmio -- e sabendo que o carro está atrás de uma delas, o concorrente tem que se decidir se permanece com a porta que escolheu no início do jogo e abre-a ou se muda para a outra porta que ainda está fechada para então a abrir.
Qual é a estratégia mais lógica? Ficar com a porta escolhida inicialmente ou mudar de porta? Com qual das duas portas ainda fechadas o concorrente tem mais probabilidades de ganhar? Porquê?
solução do problema
Uma primeira análise poderia levar a pensar que não, porque nas duas restantes portas a probabilidade de se ganhar o carro, tendo sido eliminada uma das portas, seria de 50 % para cada uma das duas restantes. Parece inútil trocar.
Mas a realidade é que trocar de porta duplica a probabilidade de ganhar o carro ! Com efeito, à partida, as probabilidades de se ganhar o carro na porta escolhida e nas duas restantes portas são 1/3 e 2/3, respectivamente. Mas não se sabe qual das duas portas não escolhidas conterá o carro e apenas se pode escolher uma única porta.
Ao ser revelado o conteúdo de uma destas duas portas, a probabilidade do prémio estar contido em ambas mantém-se igualmente em 2/3 mas agora sabe-se que a probabilidade de estar na porta revelada é igual a 0. Logo, estes 2/3 de hipótese de ganho estarão contidos integralmente na porta por abrir, que o concorrente não escolheu à partida mas que pode escolher se optar por trocar a sua opção inicial. A conclusão a tirar é que vale a pena trocar de porta porque assim se duplica a probabilidade inicial de ganhar o carro !
Este problema, por ser pouco intuitivo para a maior parte das pessoas, confundiu muita gente, inclusivamente ilustres matemáticos, na altura em que foi colocado (excepto a mulher com o maior QI do mundo, que o resolveu à primeira). É um facto que muitos deles apenas ficaram convencidos da solução após executarem uma simulação em computador para verificarem experimentalmente os referidos 2/3 de probabilidade.
terça-feira, 19 de fevereiro de 2008
Dois votos: o sistema eleitoral alemão

No fundo, é tudo muito simples: com o seu "x" no boletim de voto, os alemães decidem quem terá um mandato no Parlamento e quem ficará de fora. Mas, então, que papel representam a cláusula dos cinco por cento, os mandatos suplementares, o primeiro e o segundo votos no resultado final da eleição?
Na Alemanha, o voto não é obrigatório e, sim, facultativo. Para determinar a composição do Bundestag –num total de 598 mandatos – cada eleitor tem direito a dois votos.
O segundo voto é decisivo
Com seu primeiro voto, os eleitores escolhem o deputado que deverá representar o seu distrito eleitoral em Berlim. É o chamado "mandato directo". A maioria simples dos votos decide a obtenção do mandato em cada distrito eleitoral.Metade do número de deputados (ou seja, 299) é escohida desta maneira.
A formação das maiorias parlamentares, contudo, depende fundamentalmente do segundo voto – um voto de legenda. Com ele, os eleitores escolhem os ocupantes das 299 cadeiras parlamentares restantes e determinam também a força política de cada um dos partidos.
Lista eleitoral
Os partidos estabelecem, em cada Estado, uma lista eleitoral hierárquica com os nomes dos candidatos a serem enviados como deputados a Berlim de acordo com o número obtido de votos de legenda.
A grande importância do segundo voto decorre do facto de ser ele determinante para o número total de deputados de um partido. O total dos mandatos parlamentares é distribuído entre os partidos segundo a proporção dos respectivos votos de legenda. Deduz-se, porém, o número de mandatos directos conquistados.
Um exemplo: após o apuramento final dos votos de legenda, cabe a um determinado partido um total de 100 mandatos. Mas o partido conquistou 40 mandatos directos – os outros 60 deputados sairão, por ordem hierárquica, da lista de candidatos. Se o mesmo partido só tiver conquistado 30 mandatos directos, os 70 primeiros nomes da lista partidária serão enviados então a Berlim como deputados.
Mandatos suplementares
Até aqui, o que foi citado é a regra geral. Mas existe também um caso especial – o dos mandatos suplementares. Isto ocorre quando um partido conquista mandatos directos em número superior ao total a que teria direito de acordo com os votos de legenda obtidos.
O partido pode, então, ficar com tais mandatos excedentes, aumentando assim o número total dos deputados ao Parlamento federal alemão. Em 1994, houve um total de 16 mandatos suplementares. Nas eleições federais de 1998, o número foi um pouco menor: 13 mandatos. Na última eleição, em 2002, esse número caiu para cinco.
Cinco por cento é o mínimo
O sistema eleitoral alemão tem ainda um regulamento peculiar: a cláusula dos cinco por cento. Segundo ela, qualquer partido só obtém representação no Parlamento se obtiver um mínimo de 5% do total de votos de legenda. Isto evita que um número infindável de partidos de pequena expressão se façam representar no Bundestag, com conseqüências negativas para um trabalho parlamentar eficaz.
Mas, como todas as regras, também esta tem uma excepção. Se um partido não consegue obter 5% dos votos de legenda, mas conquista três ou mais mandatos directos, então tem o direito de se fazer representar no Parlamento. Neste caso, os seus votos de legenda são tomados como base de cálculo para o seu número total de mandatos.
domingo, 17 de fevereiro de 2008
Os algoritmos do bolo-rei
Todos conhecemos a melhor maneira de repartir um bolo entre duas pessoas, sem que nenhuma se possa queixar: uma parte e outra escolhe. O problema complica-se quando há mais de dois parceiros. Por muito trivial que pareça, os matemáticos têm tratado este problema, obtendo algoritmos de repartição eficazes.


Texto de Nuno Crato
«Quem parte e reparte, e não fica com a melhor parte, ou é tolo ou não tem arte», diz um ditado popular. É verdade: se a pessoa a fazer a divisão for também a que fizer a escolha, nada garante que um dos parceiros não fique prejudicado. Por isso, e para evitar que alguém se possa queixar do resultado da partilha, o melhor é proceder em duas etapas: um dos parceiros divide o bolo e o outro escolhe a sua fatia.
Desta forma, é do interesse do primeiro fazer a divisão da forma mais equitativa possível, pois se assim não acontecer, terá a certeza de ficar com o pior bocado. É uma sábia conjugação de situações, pois os dois parceiros, afinal ambos movidos pelo egoísmo, colaboram de forma a que nenhum fique prejudicado.
A história é muito conhecida e aplicada em várias situações do dia-a-dia, e não só na divisão de guloseimas entre crianças. O problema complica-se, contudo, se o bolo tiver de ser dividido entre mais do que dois parceiros. Como é que se há-de fazer se forem três, por exemplo? Ou se forem muito mais? E se tivermos um bolo-rei a dividir entre 20 pessoas igualmente gulosas?
O problema não é simples e os matemáticos têm vindo a desenvolver algoritmos para partilhas equitativas. Esses algoritmos, isto é, esses procedimentos sistemáticos de busca de uma solução, podem ter aplicações em áreas muito diversas, desde a partilha de heranças e divisão de obrigações pecuniárias até às negociações de desarmamento ou ao estabelecimento de fronteiras entre países.
O algoritmo «um parte, outro escolhe» pode aplicar-se a mais do que dois parceiros. Se tivermos quatro pretendentes a um bolo-rei, por exemplo, o algoritmo desdobra-se em duas etapas. Começam-se por agrupar os pretendentes ao bolo em dois grupos, com dois elementos em cada grupo. Um dos grupos divide o bolo em duas partes e o outro escolhe a sua metade. Na segunda etapa, cada par de gulosos divide a sua metade de bolo-rei ao meio, seguindo de novo o processo de um partir e o outro escolher.
É fácil ver que este método pode funcionar igualmente para oito pessoas ou, em geral, para potências de dois. Mas já não é tão simples encontrar uma solução no caso de haver três pessoas. Pensando bem, consegue-se arranjar um método que funcione nesse caso. Quer o leitor dar uma sugestão?
Os matemáticos, contudo, não gostam de soluções que apenas funcionam para casos particulares, pelo que têm procurado algoritmos mais gerais. O ideal seria encontrar um método que funcionasse com qualquer número de pessoas. Um desses métodos, proposto pelos matemáticos polacos Stefan Banach (1892-1945) e Bronislaw Knaster (1893-1980), resolve o problema com qualquer número de parceiros. É o chamado algoritmo da faca deslizante. Este caso é mais fácil de perceber com um bolo sobre o comprido, como um bolo inglês.
Os diversos pretendentes às fatias do bolo reúnem-se à sua volta enquanto uma pessoa, possivelmente um deles, pouco importa, começa a deslizar a faca sobre o bolo, a partir de um dos lados. Vai-se progredindo com a faca até que um dos parceiros diga «Pára!». Nesse momento, pára-se a faca e corta-se uma fatia, que é entregue a quem falou. O parceiro em causa fica assim com uma parte que considera ser, pelo menos, uma fracção justa do bolo - se pensasse que a faca não tinha ainda chegado a essa fracção justa, não a teria reclamado. Os outros, por seu lado, vêem o bolo ser diminuído do que consideram ser inferior ou igual a uma fracção justa - se algum deles achasse que a faca tinha já ultrapassado o momento certo, deveria ter reclamado a fatia correspondente.
Depois de o primeiro parceiro ter recolhido a sua fatia, este afasta-se do jogo, enquanto a faca continua a deslizar, até que um dos restantes parceiros diga «Pára» e recolha a sua fatia. O processo repete-se até restarem apenas dois parceiros. Nessa altura, o primeiro a falar é o que fica com a fatia reclamada e o último fica com o restante. O interessante neste processo é que, mesmo admitindo a falibilidade de cada uma das pessoas, nenhuma delas pode reclamar que está a ser prejudicada. Se o está, é por sua culpa, pois não terá falado a tempo, ou terá falado cedo demais, sem a isso ninguém a ter obrigado.
Este método parece perfeito, mas deixa de fora alguns casos interessantes. Funciona para um bolo homogéneo, mas funcionará para um bolo com constituintes diversos e irregularmente distribuídos, como é o caso do bolo-rei? Será possível arranjar um algoritmo em que todos fiquem com igual quantidade de abóbora cristalizada, de pinhões, de passas e de massa? A resposta a esta questão foi dada por um teorema que o matemático polaco Hugo Steinhaus (1887-1972) demonstrou nos anos 40 e que veio a ser conhecido pelo curioso nome de Teorema da Sanduíche de Fiambre. Considere-se um objecto tridimensional com três componentes, por exemplo, uma sanduíche com pão, queijo e fiambre - pouco importa que esses componentes estejam bem ou mal distribuídos, que se concentrem em lados diferentes ou que estejam uniformemente espalhados. O que esse resultado prova é que há sempre um plano que divide o objecto em duas partes, de tal maneira que cada uma delas contenha igual quantidade dos três componentes. Ou seja, mesmo que o fiambre e o queijo estejam mal espalhados, há sempre uma maneira de cortar a sanduíche em dois bocados rigorosamente iguais.
Quando se considera um objecto bidimensional, já a partição equitativa apenas funciona com dois componentes. Suponha-se que se espalha sal e pimenta numa mesa, por exemplo. O teorema de Steinhaus mostra que há sempre uma recta que divide a superfície da mesa em duas partes que têm iguais quantidades de sal e de pimenta. Se houver três ingredientes, suponhamos sal, pimenta e açúcar, é fácil de imaginar uma concentração em três locais diferentes de tal forma que não haja linha recta que faça a partição de forma equitativa. De forma geral, o teorema diz que em «n» dimensões há sempre um hiperplano que divide simultaneamente ao meio «n» componentes. Como parece que vivemos a três dimensões e o bolo-rei tem muito mais que três constituintes, ficamos a saber: não há faca que os reparta todos equitativamente.


Texto de Nuno Crato
«Quem parte e reparte, e não fica com a melhor parte, ou é tolo ou não tem arte», diz um ditado popular. É verdade: se a pessoa a fazer a divisão for também a que fizer a escolha, nada garante que um dos parceiros não fique prejudicado. Por isso, e para evitar que alguém se possa queixar do resultado da partilha, o melhor é proceder em duas etapas: um dos parceiros divide o bolo e o outro escolhe a sua fatia.
Desta forma, é do interesse do primeiro fazer a divisão da forma mais equitativa possível, pois se assim não acontecer, terá a certeza de ficar com o pior bocado. É uma sábia conjugação de situações, pois os dois parceiros, afinal ambos movidos pelo egoísmo, colaboram de forma a que nenhum fique prejudicado.
A história é muito conhecida e aplicada em várias situações do dia-a-dia, e não só na divisão de guloseimas entre crianças. O problema complica-se, contudo, se o bolo tiver de ser dividido entre mais do que dois parceiros. Como é que se há-de fazer se forem três, por exemplo? Ou se forem muito mais? E se tivermos um bolo-rei a dividir entre 20 pessoas igualmente gulosas?
O problema não é simples e os matemáticos têm vindo a desenvolver algoritmos para partilhas equitativas. Esses algoritmos, isto é, esses procedimentos sistemáticos de busca de uma solução, podem ter aplicações em áreas muito diversas, desde a partilha de heranças e divisão de obrigações pecuniárias até às negociações de desarmamento ou ao estabelecimento de fronteiras entre países.
O algoritmo «um parte, outro escolhe» pode aplicar-se a mais do que dois parceiros. Se tivermos quatro pretendentes a um bolo-rei, por exemplo, o algoritmo desdobra-se em duas etapas. Começam-se por agrupar os pretendentes ao bolo em dois grupos, com dois elementos em cada grupo. Um dos grupos divide o bolo em duas partes e o outro escolhe a sua metade. Na segunda etapa, cada par de gulosos divide a sua metade de bolo-rei ao meio, seguindo de novo o processo de um partir e o outro escolher.
É fácil ver que este método pode funcionar igualmente para oito pessoas ou, em geral, para potências de dois. Mas já não é tão simples encontrar uma solução no caso de haver três pessoas. Pensando bem, consegue-se arranjar um método que funcione nesse caso. Quer o leitor dar uma sugestão?
Os matemáticos, contudo, não gostam de soluções que apenas funcionam para casos particulares, pelo que têm procurado algoritmos mais gerais. O ideal seria encontrar um método que funcionasse com qualquer número de pessoas. Um desses métodos, proposto pelos matemáticos polacos Stefan Banach (1892-1945) e Bronislaw Knaster (1893-1980), resolve o problema com qualquer número de parceiros. É o chamado algoritmo da faca deslizante. Este caso é mais fácil de perceber com um bolo sobre o comprido, como um bolo inglês.
Os diversos pretendentes às fatias do bolo reúnem-se à sua volta enquanto uma pessoa, possivelmente um deles, pouco importa, começa a deslizar a faca sobre o bolo, a partir de um dos lados. Vai-se progredindo com a faca até que um dos parceiros diga «Pára!». Nesse momento, pára-se a faca e corta-se uma fatia, que é entregue a quem falou. O parceiro em causa fica assim com uma parte que considera ser, pelo menos, uma fracção justa do bolo - se pensasse que a faca não tinha ainda chegado a essa fracção justa, não a teria reclamado. Os outros, por seu lado, vêem o bolo ser diminuído do que consideram ser inferior ou igual a uma fracção justa - se algum deles achasse que a faca tinha já ultrapassado o momento certo, deveria ter reclamado a fatia correspondente.
Depois de o primeiro parceiro ter recolhido a sua fatia, este afasta-se do jogo, enquanto a faca continua a deslizar, até que um dos restantes parceiros diga «Pára» e recolha a sua fatia. O processo repete-se até restarem apenas dois parceiros. Nessa altura, o primeiro a falar é o que fica com a fatia reclamada e o último fica com o restante. O interessante neste processo é que, mesmo admitindo a falibilidade de cada uma das pessoas, nenhuma delas pode reclamar que está a ser prejudicada. Se o está, é por sua culpa, pois não terá falado a tempo, ou terá falado cedo demais, sem a isso ninguém a ter obrigado.
Este método parece perfeito, mas deixa de fora alguns casos interessantes. Funciona para um bolo homogéneo, mas funcionará para um bolo com constituintes diversos e irregularmente distribuídos, como é o caso do bolo-rei? Será possível arranjar um algoritmo em que todos fiquem com igual quantidade de abóbora cristalizada, de pinhões, de passas e de massa? A resposta a esta questão foi dada por um teorema que o matemático polaco Hugo Steinhaus (1887-1972) demonstrou nos anos 40 e que veio a ser conhecido pelo curioso nome de Teorema da Sanduíche de Fiambre. Considere-se um objecto tridimensional com três componentes, por exemplo, uma sanduíche com pão, queijo e fiambre - pouco importa que esses componentes estejam bem ou mal distribuídos, que se concentrem em lados diferentes ou que estejam uniformemente espalhados. O que esse resultado prova é que há sempre um plano que divide o objecto em duas partes, de tal maneira que cada uma delas contenha igual quantidade dos três componentes. Ou seja, mesmo que o fiambre e o queijo estejam mal espalhados, há sempre uma maneira de cortar a sanduíche em dois bocados rigorosamente iguais.
Quando se considera um objecto bidimensional, já a partição equitativa apenas funciona com dois componentes. Suponha-se que se espalha sal e pimenta numa mesa, por exemplo. O teorema de Steinhaus mostra que há sempre uma recta que divide a superfície da mesa em duas partes que têm iguais quantidades de sal e de pimenta. Se houver três ingredientes, suponhamos sal, pimenta e açúcar, é fácil de imaginar uma concentração em três locais diferentes de tal forma que não haja linha recta que faça a partição de forma equitativa. De forma geral, o teorema diz que em «n» dimensões há sempre um hiperplano que divide simultaneamente ao meio «n» componentes. Como parece que vivemos a três dimensões e o bolo-rei tem muito mais que três constituintes, ficamos a saber: não há faca que os reparta todos equitativamente.
sábado, 16 de fevereiro de 2008
O Teorema das Quatro Cores

O teorema do mapa de quatro cores diz que não são necessárias mais de quatro cores para pintar qualquer mapa plano concebível, de países reais ou imaginário, de tal modo que dois países vizinhos não tenham a mesma cor.
A demonstração deste teorema é considerado um dos maiores feitos da matemática moderna. Este foi um dos primeiros grandes teoremas a ser provado usando um computador, no entanto esta prova não é ainda aceite por todos os matemáticos visto ninguém o ter conseguido demonstrar usando apenas papel e caneta.
Em meado do século XIX os matemáticos pensavam que este teorema era verdadeiro, tendo sido proposto como conjectura em 1852 por Francis Guthrie, que se apercebeu enquanto pintava o mapa dos condado de Inglaterra que apenas necessitava de quatro cores. Durante mais de 100 anos matemáticos de todo o mundo atacaram o problema com unhas e dentes tendo sempre falhado na sua demonstração.
No livro O Homem Que Só Gostava de Números, Paul Hoffman conta a história de um matemático, chamado E.F. Moore, que teve durante uns tempos como objectivo de vida encontrar um contra exemplo. Todos os dias chegava ao trabalho, na AT&M, com uma folha gigante de papel com mais de um metro quadrado onde tinha cuidadosamente desenhado um mapa com milhares de países. "Hoje vou conseguir", dizia ele pela manhã, "vou provar que são precisas 5 cores". Ao fim do dia saía desiludido. Mas na manhã seguinte lá estava ele com um lençol cheio de minúsculos e intrincados países imaginários.
Foi apenas em 1976 que a conjectura foi finalmente demonstrada por Kenneth Appel e Wolfgang Haken na Universidade de Illinois. Quando isto aconteceu reza a história que muitos professores de matemática terão interrompido as sua aulas para abrir uma garrafa de champanhe. No entanto muitos matemáticos não ficaram contentes, pois a descoberta tinha sido feita usando 3 supercomputadores durante mais de 1000 horas. Na realidade Appel e Haken demonstraram que todos os mapas possíveis eram variações de 1500 tipos fundamentais, e os computadores conseguiram pintá-los a todos com um máximo de quatro cores. Há quem acredite ainda que este teorema pode ser demonstrado com papel, lápis e umas poucas folhas.

Bibliografia:
- Four color theorem, Wikipédia
- O Homem Que Só Gostava de Números, Ciência Aberta, Nº105, Gradiva.
Subscrever:
Mensagens (Atom)
AS CLASSES DE GINÁSTICA - o método de Hamilton
Três classes de ginástica de um clube decidem constituir uma associação que defenda os seus interesses. A assembleia será constituída por 2...

-
Num grafo, chama-se circuito de Hamilton a um caminho que começa e acaba no mesmo vértice, passando por todos os vértices uma única vez. Alg...
-
Grafo - estrutura matemática usada para representar as relações entre as coisas ou objectos. Os grafos possuem nós ou vértices (coisas/ob...
-
Tabela para cálculo do IMT em 2008, aplicável no Continente É calculado multiplicando a "Taxa Marginal" pelo valor de transacção d...

