O problema de Monty Hall

O problema de Monty Hall surgiu, nos anos 70, de um concurso televisivo americano – Let’s Make a Deal.
O jogo consiste no seguinte: Monty Hall, o apresentador do concurso, apresenta 3 portas fechadas aos concorrentes, sabendo que atrás de uma delas existe um carro e que as outras apenas têm prémios simbólicos (um animal..., um aspirador, uma torradeira ou outros semelhantes).
1 - Na 1ª etapa o concorrente escolhe uma porta;
2 - De seguida, o apresentador abre uma das outras duas portas que o concorrente não escolheu,
sabendo à partida que o carro não se encontra aí;
3 - Agora com duas portas apenas, e sabendo que o carro está atrás de uma delas, ao concorrente é
dada a possibilidade de alterar a sua escolha. Assim, deve decidir se permanece com a porta
que escolheu no início do jogo ou se muda para a outra porta que ainda está fechada.

Qual a opção mais vantajosa? Trocar de portas ou manter a escolha inicial? Ou será que é indiferente, e porquê?

Realmente não é assim tão indiferente mudar ou ficar na mesma porta.
À partida quando se escolheu uma das portas havia 1/3 de probabilidade de ganhar o carro. Não existe
razão nenhuma para essa probabilidade mudar após o apresentador ter aberto uma das portas que não
era premiada. As outras duas portas não escolhidas tinham em conjunto 2/3 de probabilidade de
ocultarem o carro, e quando uma dessa portas é aberta (por não ter prémio) a porta não escolhida que
continua fechada passa a ter 2/3 de probabilidade de ser a porta com o carro.

Probabilidade de ganhar:
2/3 se trocar de porta
1/3 se não trocar de porta

Este é um problema “viciado”, pois só o apresentador sabe onde está o carro e qual a porta a abrir.

Modelos Populacionais - Modelo Exponencial / Modelo de Crescimento Linear

A POPULAÇÃO DE NENÚFARES
Uma determinada espécie de nenúfares tem uma taxa de crescimento diária de
7%. Num certo lago, deu-se início a este tipo de população colocando 100
nenúfares.
1. Ao fim de quantos dias a população duplicou?
2. Quantos anos terão de decorrer para que a população torne a duplicar?
E para existirem 800? E 1600?
3. Represente graficamente a evolução da população de nenúfares.
4. Determine um modelo para esta situação.


A REPOVOAÇÃO DO LAGO
A preservação da Natureza e os cuidados a ter com a vida selvagem tem-se tornado, cada vez mais, assuntos que preocupam as civilizações contemporâneas. Com o objectivo de restabelecer a fauna de um certo lago natural, um departamento de investigação decidiu repovoá-lo com 3000 trutas.
Analisada a adaptação das trutas ao lago, constatou-se que esta população tem uma taxa anual de decrescimento de 20 % devido à pesca e a factores naturais, como a morte. Para combater a diminuição, a equipa decidiu acrescentar anualmente 1000 trutas.
Com o objectivo de conhecer a evolução desta população, reflicta e responda às seguintes questões.
1. Determine a população de trutas um ano depois de se ter iniciado o processo de repovoação.
2. Determine a população de trutas no lago ao fim de cinco anos.
3. Represente por uma tabela e graficamente a evolução das trutas durante os primeiros 25 anos.
4. Quando é que as alterações na população são mais significativas: ao fim de 5 ou ao fim de 25 anos?
5. Pronuncie-se sobre a evolução da população.

Problemas de Distribuição Normal

1) A concentração de um poluente em água que sai de uma fábrica tem distribuição
N(8,1.5). Qual a probabilidade, de que num determinado dia, a concentração do poluente exceda o limite de 10 ppm?

solução: 9,1%

2) A concentração de cádmio em cinzas de um certo lixo radioactivo tem distribuição N(1,0.72). Quai é a probabilidade de que uma amostra aleatória das cinzas tenha uma concentração de cádmio entre 0.5 e 1.75 ppm?

solução: 60,8 %

Modelação Financeira

Regime de Capitalização Simples

Taxa de juro - é o valor produzido por 100 unidades de capital numa unidade de tempo e representa-se por i.

Juro simples - é aquele que não é capitalizado, isto é, quando o juro não rende juro nos vencimentos da aplicação.

Cn = C + Cni
Cn = C (1+ ni)

Cn - Capital acumulado
C - Capital inicial
Cni - Juro
i - Taxa de juro referente ao período de capitalização
n - Nº de períodos de capitalização.

Regime de Capitalização Composta

Juro composto - o valor do juro é capitalizado no investimento, ou seja, quando os juros passam a render juros no período seguinte.

De um modo geral: Cn = C (1 + i)n^2
Cn - Capital acumulado
C - Capital inicial
i - Taxa de juro referente ao período de capitalização
n - Nº de períodos de capitalização.

Empréstimos

A fórmula seguinte permite calcular a mensalidade a pagar por um empréstimo de capital com a taxa de juro i:
a = C *[((1 + i)^n * i) / ((1 + i)^n - 1)]

a - mensalidade
i - taxa de juro mensal
C - capital a pagar
N - nº de meses.

Intervalos de confiança

Intervalo de confiança para o valor médio de uma variável normal X, admitindo que se conhece o desvio-padrão da variável:

]média amostral - z * (desvio-padrão / raíz quadrada de n); média amostral + z * (desvio-padrão / raíz quadrada de n)[

Intervalo de confiança não conhecendo o desvio-padrão populacional:

]média amostral - z * o desvio-padrão amostral sobre a raíz da dimensão da amostra; média amostral + z * o desvio-padrão amostral sobre raíz da dimensão da amostra[.

Margem de erro

A margem de erro é igual a metade da amplitude do intervalo de confiança.

E = z * raíz quadrada de [^p(1-^p)/n]
E= z * (desvio-padrão/ raíz quadrada de n)

n - dimensão da amostra
^p - proporção amostral
z - valor relacionado com o nível de confiança mais usual.


Para diminuir o erro temos 2 possibilidades:
- aumentar n;
- diminuir a confiança, diminuindo assim o valor de z.

Nível de confiança e z:
90%... z = 1,645
95%... z = 1,960
99%... z = 2,576

Método de run-off sequencial

Algoritmo:
-Cada eleitor vota num candidato, mas ordena os restantes por ordem decrescente de preferência no mesmo boletim de voto.
-Se um candidato obtém a maioria absoluta com as primeiras preferências é eleito.
-Se nenhum candidato obtém a maioria absoluta, elimina-se o candidato menos votado.
-Nos boletins dos que votaram no candidato menos votado (o eliminado) procuram-se as segundas preferências.
-Faz-se a contagem de votos dessa 2ª preferência.
-Juntam-se os votos da 2ª preferência aos votos que os candidatos não eliminados já tinham.
-O processo repete-se até se encontrar um candidato com maioria absoluta.

Método de eliminação de run-off dos 2 candidatos mais votados

Algoritmo:
-Ganha o candidato com a maioria absoluta na 1ª preferência, caso contrário, eliminam-se os candidatos, com excepção dos 2 mais votados na 1ª preferência.
-De seguida, nos boletins dos que votaram nos candidatos que foram eliminados procuram-se as segundas preferências e os votos das segundas preferências juntam-se aos votos dos candidatos que restam.
-O vencedor é o que obtiver mais votos.

Teoria da Partilha - Método da Licitação Secreta

Este método pode aplicar-se nos casos em que se pretende dividir bens por 2 ou mais pessoas.
- Os bens podem ser ou não divisíveis.
- Este método pressupõe a existência de dinheiro para acertos e compensações.
- No caso de não-existência de dinheiro vai ser necessãrio constituir um empréstimo e como este está sujeito a juros o método de partilha pode não ser considerado justo.






Algoritmo:
1-Cada interveniente atribui secretamente um valor a cada um dos bens, calculando-se assim a parte que cada um entende ser justo receber.
2-O bem é atribuído à pessoa que mais o valorizou.
3-Calcula-se quanto é que cada um vai receber em dinheiro, fazendo a diferença entre o valor que entendia ser justo receber (1/n dos bens e do dinheiro) e o valor dos bens que recebeu, sendo n o nº de intervenientes.
4-Calcula-se 1/n do dinheiro sobrante que é igual a 1/n (dinheiro - soma dos valores que cada um vai receber em dinheiro).
5-Cada interveniente recebe bens + dinheiro+ 1/n do dinheiro sobrante.

Algoritmo de Kruskal para a árvore geradora

Algoritmo:
1)Encontrar a aresta com menor peso (se houver mais do que uma, escolhemos ao acaso) e "marcá-la" a cor.
2)Encontrar a aresta seguinte com menor peso que não feche um circuito e marcá-la a cor; se a aresta a escolher fechar o circuito, não consideramos essa aresta.
3)Repetir os passos anteriores até que todos os vértices tenham sido cobertos pela árvore.

Árvores

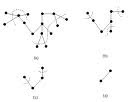
As árvores são uma classe de grafos que não admite circuitos.





Propriedades das árvores:
1-Se um grafo é uma árvore, há um e só um caminho entre 2 quaisquer vértices; reciprocamente, se houver um único caminho que ligue 2 quaisquer vértices, então o grafo é uma árvore.
2-Numa árvore, cada aresta é uma ponte; reciprocamente, se cada aresta de um grafo conexo é uma ponte, então o grafo é uma árvore.
3-Uma árvore com n vértices tem n -1 arestas.
4-Um grafo conexo com n vértices e n - 1 arestas é uma árvore.

Grafos Hamiltonianos. Algoritmos: Vizinho Mais Próximo e Peso das Arestas

Num grafo, chama-se circuito de Hamilton a um caminho que começa e acaba no mesmo vértice, passando por todos os vértices uma única vez.



Algoritmo do vizinho mais próximo
1)Define-se o vértice de partida.
2)Segue-se para o vértice mais próximo (de menor peso) que ainda não tenha sido visitado (devemos ter em conta que se houver 2 vértices com o mesmo peso, a escolha é aleatória).
3)Só se pode fechar o circuito quando todos os vértices tiverem sido visitados.

Algoritmo do peso das arestas
1)Ordenam-se as arestas pelos seus pesos.
2)Escolhem-se sucessivamente as arestas de menor peso que verifiquem as seguintes condições: um vértice nunca poderá aparecer 3 vezes e nunca se fecha um circuito havendo vértices por visitar.
3)Ordena-se a solução conforme o vértice de partida escolhido.

Grafos Eulerianos

Um circuito de Euler é um circuito que passa uma única vez em cada aresta do grafo.

Um grafo diz-se euleriano se admite um circuito de Euler.

Um caminho de Euler ou um caminho euleriano é um caminho que passa uma única vez em cada aresta do grafo.

Um grafo é euleriano se e só se é conexo e todos os seus vértices são de grau par.

Um grafo admite um caminho euleriano se e só se é conexo e no máximo 2 dos seus vértices têm grau ímpar. Tal caminho terá início num dos vértices de grau ímpar e termina no outro vértice de grau ímpar.

Ao processo que consiste em transformar um grafo que não é euleriano num grafo de Euler, duplicando arestas, chama-se eulerizar um grafo.

Distribuição de amostragem e Teorema do Limite Central

Valor médio é a medida de localização do centro da distribuição dos valores assumidos por uma dada variável aleatória, cuja estimativa será a média de uma amostra de observações dessa variável.
A proporção ou frequência relativa com que se verifica uma determinada característica na população tem como estimativa a proporção de vezes que essa característica se confirma nos elementos de amostra recolhida dessa população.

Teorema do limite central:
Suponhamos que se recolhe uma amostra de dimjensão n de uma população muito grande, X , com valor médio e desvio-padrão.
Então, se a dimensão da amostra for suficientemente grande (n superior ou igual a 30), a distribuição da amostragem da média pode ser aproximada por uma distribuição normal com valor médio e desvio-padrão: desvio-padrão sobre a raíz de n.
Dada uma população de valor médio e desvio-padrão, não necessariamente normal, a distribuição das médias das amostras de dimensão n: tem média igual ao valor médio da população; o seu desvio-padrão é desvio-padrão sobre raíz de n e, portanto, diminui quando aumenta n; quando n é maior ou igual a 30, é aproximadamente normal.

Probabilidade Condicionada. Acontecimentos Independentes.

A formiga e a aranha


Uma formiga desloca-se ao longo de um caminho que, como a figura mostra, vai apresentando bifurcações. A formiga nunca inverte a sua marcha. Ao chegar a uma bifurcação, opta 70% das vezes pelo caminho da esquerda.


Qual é a probabilidade de a formiga ser apanhada pela aranha?

1) 0,14

2) 0,21

3) 0,42

4) 0,49